Specific Heat and Heat Capacity
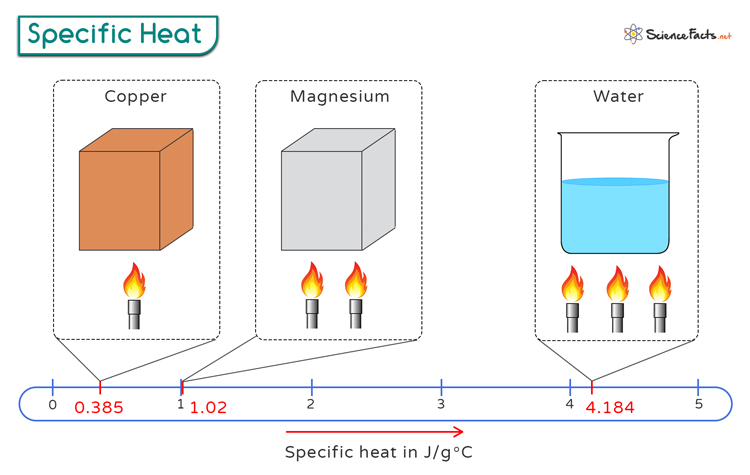
Specific heat is defined as the amount of heat required to raise the temperature of a unit mass of a substance by one degree Celsius. It plays a crucial role in understanding how different materials respond to heating and cooling and describes their ability to store and release thermal energy. For example, water has a higher specific heat than metals. It means that more heat is required to raise water’s temperature by one degree than metals’, as shown in the image below.
On the other hand, heat capacity is the amount of heat required to increase the temperature of the entire substance by one degree Celsius.
Specific Heat and Heat Capacity Formula
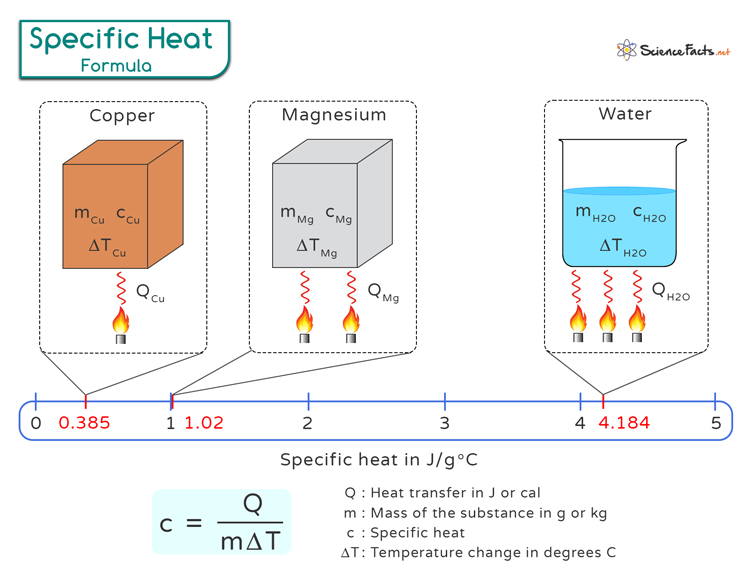
The specific heat can be calculated from the amount of heat transferred into and out of a substance. The heat transfer equation provides a quantitative relationship between heat transfer, substance’s mass, specific heat, and temperature change. It is shown as follows:
Where
- Q represents the heat transfer in Joules (J) or calories (cal).
- m denotes the mass of the substance in grams (g) or kilograms (kg) being heated or cooled.
- c is the specific heat
- ΔT represents the temperature change in degrees Celsius (∘C) of the substance
This formula assumes no phase change occurs during heating or cooling processes and applies specifically to substances with constant specific heat within a given temperature range.
Rearranging the above equation, one can find the expression for specific heat.
The heat capacity (C) can be calculated by multiplying the specific heat with the mass. Therefore,
Units
The unit of specific heat is Joules per gram per degree Celsius or J/g∙∘C. Another unit of specific heat is calories per gram per degree Celsius or J/cal∙∘C. The temperature change (∆T) in the Celsius (C) scale is the same as that in the Kelvin (K) scale, although the temperature values differ. Therefore, one can replace ∘C with K. In that case, the SI unit of specific heat is Joules per kilogram per degree Kelvin or J/kg∙K.
The unit of heat capacity is J/∘C or cal/∘C.
Molar Specific Heat
The specific heat of a substance can also be described in terms of its molar amount. In that case, we use a term called molar specific heat. It is defined as the amount of heat required to change the temperature of one mole of a substance by one degree. It is represented in the unit of Joules per mole per degree Celsius or J/mol∘C.
Specific Heat Table
The specific heat values can be calculated for different substances from the above formula. Below is a table that shows the values for a few common substances:
| Substance | Specific Heat (J/g∙°C) at 25 °C |
| Hydrogen | 14.3 |
| Helium | 5.193 |
| Water | 4.184 |
| Ethanol | 2.450 |
| Ice | 2.090 |
| Steam | 2.020 |
| Nitrogen | 1.040 |
| Magnesium | 1.02 |
| Air | 1.006 |
| Oxygen | 0.918 |
| Aluminum | 0.897 |
| Glass | 0.840 |
| Carbon dioxide | 0.839 |
| Sand | 0.830 |
| Steel | 0.466 |
| Iron | 0.449 |
| Nickel | 0.444 |
| Zinc | 0.388 |
| Copper | 0.385 |
| Brass | 0.380 |
| Silver | 0.240 |
| Tin | 0.227 |
| Mercury | 0.140 |
| Gold | 0.129 |
| Lead | 0.128 |
Water has a particularly high specific heat compared to many other substances. Its specific heat capacity is 4.184 J/g°C, which means it takes 4.184 Joules of energy to raise the temperature of 1 gram of water by 1 degree Celsius. Let us discuss the significance of this remarkable property of water.
Specific Heat of Water
Water has an exceptionally high capacity to absorb and retain heat energy without undergoing large temperature changes. This property is significant in thermoregulation in nature and human-made systems.
Thermoregulation is the process by which living organisms maintain their internal body temperature within a narrow range despite fluctuations in the external environment. In nature, bodies of water such as oceans, lakes, and rivers act as thermal regulators by absorbing excess heat during the daytime and slowly releasing it at night. This helps maintain stable temperatures in surrounding areas and supports diverse ecosystems.
Understanding water’s specific heat is crucial for designing efficient heating and cooling artificial systems like car radiators and hot water pipes. Water’s ability to store large amounts of thermal energy makes it an ideal medium for transferring heat between different areas while minimizing temperature fluctuations.
Difference Between Specific Heat and Heat Capacity
Below is a table summarizing the difference between specific heat and heat capacity.
| Property | Specific Heat | Heat Capacity |
| Definition | The amount of heat required to raise the temperature of a unit mass of a substance by one degree Celsius (or Kelvin). | The amount of heat required to raise the temperature of a given amount of a substance by one degree Celsius (or Kelvin). |
| Units | J/g∙°C | J/°C |
| Mass dependency | Does not depend on the mass of the substance | Depends on the mass of the substance |
| Equation | c = Q/m∆T | C = Q/∆T |
| Example | Water has a specific heat of approximately 4.18 J/g∙°C. | A pot of 10 kg of water will require 10 x 4.18 = 41.8 J of heat to increase its temperature by one degree Celsius. |
Example Problems with Solutions
Problem 1: A 200 g piece of aluminum initially at 80°C is dropped into 400 mL of water at 20°C. If the final temperature of the system is 40°C, calculate the heat transferred to the water. The specific heat of aluminum is 0.9 J/g∙°C, and the specific heat of water is 4.18 J/g∙°C.
Solution:
The heat transfer equation is given by:
Heat lost by aluminum is:
\[ q_{\text{Al}} = m_{\text{Al}} \cdot c_{\text{Al}} \cdot \Delta T_{\text{Al}} \]
\[ q_{\text{Al}} = (200 \, \text{g}) \cdot (0.9 \, \text{J/g°C}) \cdot (40 \, \text{°C} – 80 \, \text{°C}) \]
\[ q_{\text{Al}} = -7200 \, \text{J} \]
The negative sign implies that aluminum loses heat to water. Therefore, the heat transferred to water is 7200 J.
Problem 2: A 150 g piece of copper is heated from 20°C to 100°C. Calculate the heat energy absorbed by the copper. The specific heat of copper is 0.39 J/g∙°C.
Solution:
The heat transfer equation is given by:
\[ q = m \cdot c \cdot \Delta T \]
\[ q_{\text{copper}} = m_{\text{copper}} \cdot c_{\text{copper}} \cdot \Delta T_{\text{copper}} \]
\[ q_{\text{copper}} = (150 \, \text{g}) \cdot (0.39 \, \text{J/g°C}) \cdot (100 \, \text{°C} – 20 \, \text{°C}) \]
\[ q_{\text{copper}} = 4680 \, \text{J} \]
Therefore, the heat absorbed by copper is 4680 J.
-
References
Article was last reviewed on Sunday, August 11, 2024