Solenoid Magnetic Field
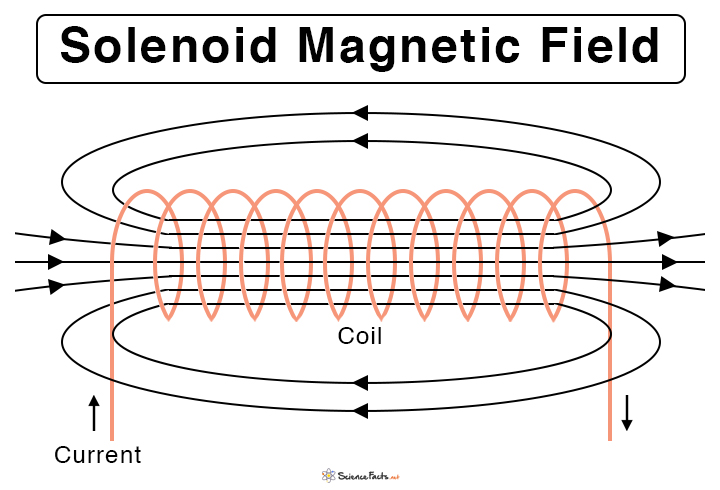
A solenoid is a conductor that is wound into a coil of many turns like a helix. The winding is adequately tight so that each turn is well approximated as a circular wire loop lying in a plane perpendicular to the solenoid’s axis.
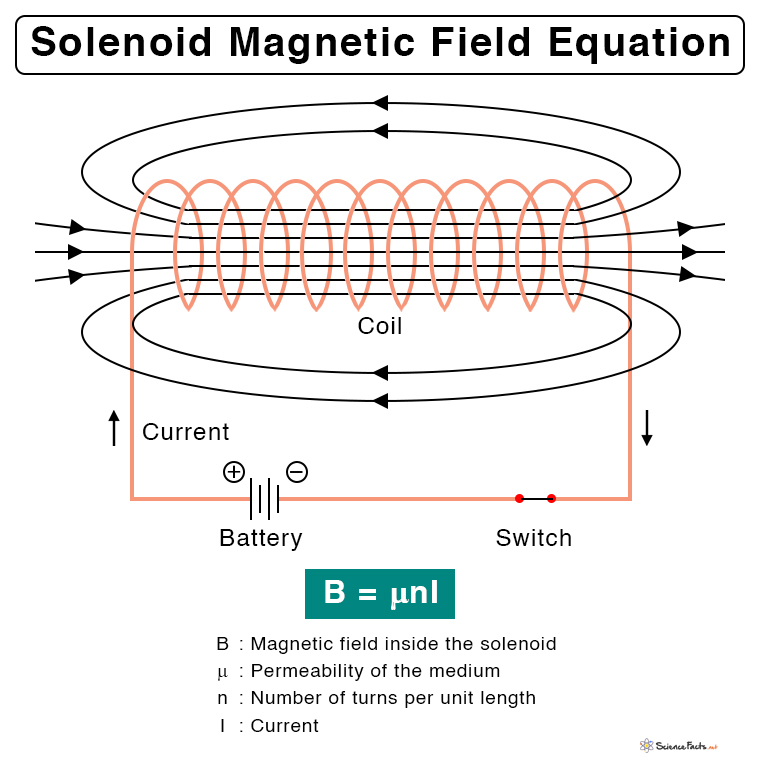
A solenoid can be used as an electromagnet when the ends are connected to a battery. A current passing through it induces a controlled magnetic field whose direction is given by the right-hand rule. The magnetic field can be enhanced by wrapping the wire around a solid metallic core, typically iron, forming a medium for the field to flow. However, the loops of wire are kept insulated from one another.
Solenoid Magnetic Field Equation
Applying Ampere’s Law to Derive the Equation
The magnetic field of a solenoid can be derived using Ampere’s law. This law gives a mathematical relationship between the magnetic field and the current flowing through a conductor.
Where
To calculate the magnetic field, we imagine a circle that encloses the current. Then, take the dot product of the magnetic field and an infinitesimal length of the circle and integrate it over the entire circle.
Magnetic Field Inside the Solenoid
The magnetic field inside a solenoid is given by,
Where,
n: Number of turns of the coil per unit length or turn density
I: Current passing through the solenoid
μ: Permeability of the metallic core
If the core is hollow, then the medium is absent. The equation is given by,
Where,
μo: Permeability of air or vacuum
Here, n is the number of turns of the coil per unit length of the solenoid. The above equation is suitable for an infinitely long solenoid. For a solenoid of finite length, the equation can be written as,
Where,
N: Total number of turns of the solenoid
L: Length of the solenoid
n = N/L: Density of turns
From the above equations, it can be seen that the magnetic field inside a solenoid is,
- Proportional to the number of turns or turn density
- Proportional to the current
- Does not depend on the distance from the axis
The magnetic field inside the solenoid remains constant and does not depend on the position. Therefore, the magnetic field is uniform throughout the inside of the solenoid. The small magnetic fields caused by the current in each turn of the coil add together to make a strong field. The presence of ferromagnetic material like iron, with high permeability, increases the field strength.
Magnetic Field Outside the Solenoid
The magnetic field lines exist outside the solenoid. However, they are not as dense as inside. Therefore, the flux density is much lower. Since the magnetic flux density measures the strength of the magnetic field, the field outside is negligible or zero. Using Ampere’s law to derive the magnetic field will yield the same result.
Direction of Magnet Field Lines
The magnetic field is uniform inside the solenoid and close to zero outside. It is similar to the magnetic field of a bar magnet having a north pole at one end and a south pole at the other. The polarity of the solenoid depends upon the direction of current flow. Suppose the current flowing around the solenoid circuit is clockwise. Then, the direction of the magnetic lines of force inside the solenoid is from left to right. If the direction of the current is reversed, the polarity will reverse as well.
The magnetic lines of force are also analogous to that of a bar magnet. They are straight and parallel and follow a longitudinal path inside the solenoid. Outside, the lines diverge and flow in the opposite direction to inside and complete the loop.
-
References
Article was last reviewed on Thursday, February 2, 2023