Single-Slit Diffraction

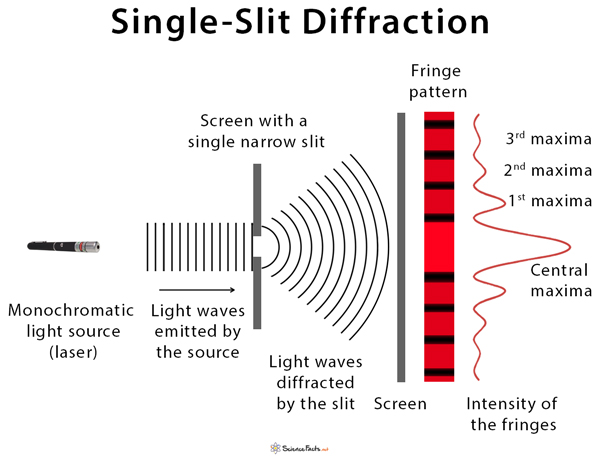
Single-slit diffraction is the most straightforward experimental setup where diffraction effects can be observed. When light passes through a slit whose width is on the order of the wavelength of light, a distinct diffraction pattern is observed on a screen that is kept at a certain distance from the slit.  The intensity is a function of the angle through which the rays bend.

Huygens’ Principle

According to Huygens’ principle, every unobstructed point on a wavefront will act as a source of secondary spherical waves. The new wavefront is the surface tangent to all the secondary spherical waves. Therefore, each part of the slit can be thought of as an emitter of waves.

All the waves passing through the slit interfere to produce a diffraction pattern consisting of bright and dark fringes. The bright fringes are due to constructive interference, and the dark areas are due to destructive interference. A number represents the order of the bright and dark fringes. The intensities of the fringes consist of a central maximum surrounded by maxima and minima on its either side. The central maximum is brighter than the other maxima. The maxima rapidly decrease as one moves further from the center.

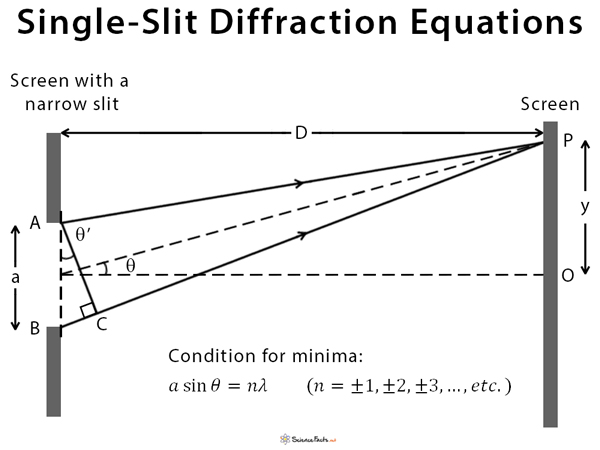
In order to study the diffraction pattern on a screen, the single-slit experiment is employed. Consider a monochromatic source of light that passes through a slit AB of width a as shown in the figure. At point P on the screen, the secondary waves interfere destructively and produce a dark fringe. Let D be the distance between the slit and the screen, and y be the distance between point P and point O, the center of the screen. AC is perpendicular to BP. Let θ be the angle of diffraction, and θ’ is the angle BAC.

We assume that the screen is at a considerable distance from the slit, i.e., D >> a. Hence,

θ = θ’

And,

sin θ ≈ tan θ ≈ θ = y/D

The path difference between the two rays AP and BP is given by,

Δ = BP – AP = BC

In the right-angled triangle BCA,

sin θ’ = sin θ = BC/BA

BC = BA sin θ = a sin θ

Therefore,

Δ = a sin θ

Diffraction Minima

The condition for minima or dark fringe is,

Path difference = integral multiple of wavelength

or, Δ = nλ (n=±1, ±2, ±3, … , etc.)

or, a sin θ = nλ

or, ay/D = nλ

or, y_n = nλD/a

This equation gives the distance of the n-th dark fringe from the center.

The fringe width is given by,

β  = y_n+1 – y_n = (n+1)λD/a  –  nλD/a

or, β = λD/a

Diffraction Maxima

The condition for maxima or bright fringe is,

Path difference = non-integral multiple of wavelength

or, Δ = (n+1/2)λ (n=±1, ±2, ±3, … , etc.)

or, a sin θ = (n+1/2)λ

or, ay/D = (n+1/2)λ

or, y_n = (n+1/2)λD/a

The intensity of single-slit diffraction is given by,

I = I₀ [sin (π a sin θ/λ)/( π a sin θ/λ)]²

Single-Slit Diffraction vs. Double-Slit Diffraction
Single-Slit Diffraction	Double-Slit Diffraction
Consist of one slit	Consist of two slits
Waves that originate within the same slit interfere	Slits are so small that each one is considered as a single light source, and the interference of waves originating within the same slit can be neglected
The fringes are broad and not as sharp as double-slit	The fringes are narrow and sharp
All bright fringes are visible	Some bright fringes are missing since they suppressed by the minima of a single-slit interference pattern
Intensity: I = I0 [sin (π a sin θ/λ)/( π a sin θ/λ)]2	Intensity: I = I0 cos2 [π d sin θ/λ] [sin (π a sin θ/λ)/( π a sin θ/λ)]2