Radius of Gyration

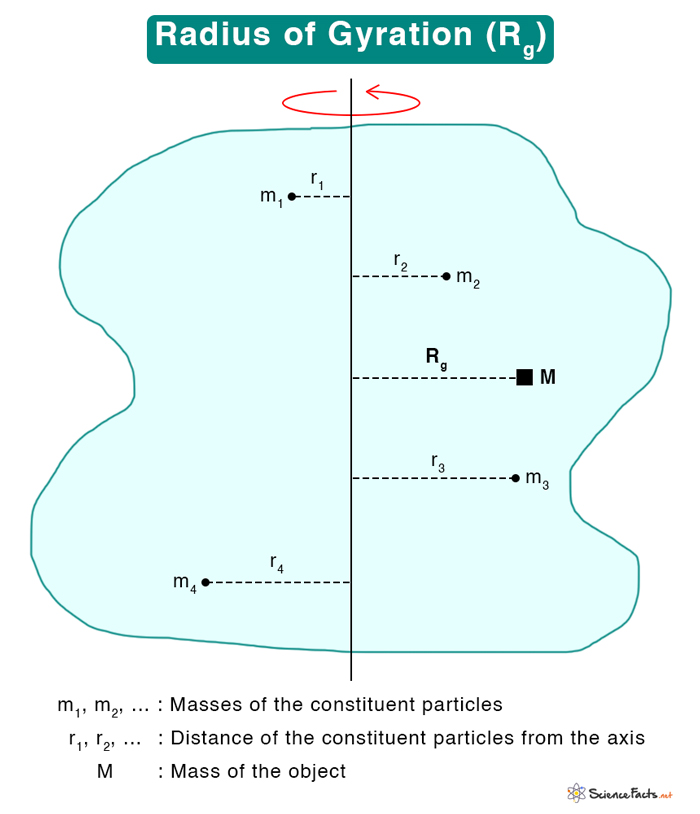
The radius of gyration of a solid body is the radial distance from an axis at which the body’s mass is assumed to be concentrated. The moment of inertia at that point is equal to the moment of inertia of the body’s actual mass about the axis.

Formula

Mathematically, the radius of gyration is the root mean square distance of the object’s constituent particles from the given axis. Suppose an object consists of n particles with masses m₁, m₂, …, m_m whose distances from a common axis are r₁, r₂, r₃, …, r_n. The moment of inertia of the object about the axis of rotation is given by

\[ I = m_1{r_1}^2 + m_2{r_2}^2 + m_3{r_3}^2 + \ldots + m_n{r_n}^2 \]

If the particles have the same mass, m, then the above equation reduces to

\[ I = m ({r_1}^2 + {r_2}^2 + {r_3}^2 + \ldots + {r_n}^2) \]

Suppose M is the total mass of the object. Then, M = nm. Therefore,

\[ I = \frac{M}{n} ({r_1}^2 + {r_2}^2 + {r_3}^2 + \ldots + {r_n}^2) \]

The moment of inertia of a concentrated mass about an axis at a distance R_g from the axis is MR_g². Here, R_g is the radius of gyration. Then,

\[ M{R_g}^2 = \frac{M}{n} ({r_1}^2 + {r_2}^2 + {r_3}^2 + \ldots + {r_n}^2) \\ R_g = \sqrt{\frac{{r_1}^2 + {r_2}^2 + {r_3}^2 + \ldots + {r_n}^2}{n}} \]

Therefore, the radius of gyration of a body about a given axis is the root mean square distance of its constituent particles from the axis of rotation. Its SI unit is meter or m.

Applications

The radius of gyration is used to study the behavior of various structures under compression along an axis. It is used to predict buckling in beams and rods.

In structural engineering, the radius of gyration is used to estimate the stiffness of a column. It describes the cross-sectional area distribution in a column around its centroidal axis with the body’s mass. The following formula gives the radius of gyration.

\[ R_g = \sqrt{\frac{I}{A}} \]

I is the second moment of inertia, and A is the cross-sectional area.

In classical mechanics, the moment of inertia I_axis is a scalar quantity. The radius of gyration r_g can be calculated for a mass m using the following equation:

\[ r_g = \sqrt{\frac{I_{axis}}{m}} \]

Example Problems

Problem 1. Find the radius of gyration of a disc of mass M and radius R rotating about an axis passing through the center of mass and perpendicular to the plane of the disc.

Solution. The moment of inertia of a disc of mass M rotation about an axis passing through its center is

I = ½ MR²

The radius of gyration is given by

\[ r_g = \sqrt{\frac{I_{axis}}{m}} = \sqrt{\frac{MR^2}{2M}} = \frac{R}{\sqrt{2}} = 0.707 \hspace{0.1 cm} \]

Problem 2. A thin uniform rod of length 1 m and mass 1 kg is rotating about an axis passing through its center and perpendicular to its length. Calculate the rod’s radius of gyration about an axis passing through a point midway between the center and its edge perpendicular to its length.

Solution

The moment of inertia of the rod about its center is

I_C = ML²/12

From the parallel axis theorem

I = I_C + Mh²

=> I = ML²/12 + M(L/4)² = (7/48) ML² = (7/48) x 1 kg x 1 m² = 0.1458 kgˑm²

The radius of gyration is given by

\[ r_g = \sqrt{\frac{I_{axis}}{M}} = \sqrt{\frac{ 0.1458 \hspace{0.1cm} kg \cdot m^2}{1 \hspace{0.1cm} kg}} = 0.3818 \hspace{0.1cm} m \]

References
- 1. Radius of Gyration – Eng.yale.edu
  2. Center of Mass and Radius of Gyration – Charmm-gui.org
  3. Radius of Gyration – Dlsweb.rmit.edu.au
  4. Radius of Gyration – Ccrma.stanford.edu