Planck’s Law

Planck’s law explains the spectral density of blackbody radiation as a function of its equilibrium temperature. It is named after German physicist Max Planck, who derived the law in 1900. Planck assumed that the radiation source is atoms that oscillate, and the vibrational energy of the atomic oscillators comes in discrete packets called quanta.

Planck hypothesized that when an oscillator jumps from a higher energy state, E_1, to a low energy state, E_2, the difference in energy between the two states is proportional to the frequency ν at which the radiation is emitted. Mathematically, the following equation shows how much is one quantum of radiation.

ΔE = E₂ – E₁ = hν

Where h is called Planck’s constant, its value is 6.67 x 10^-34 J s.

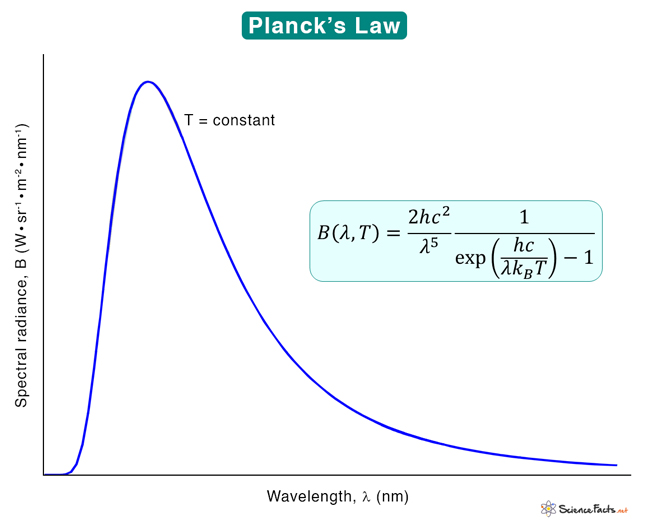
Planck’s Law Formula

The spectral radiance of a body represents the amount of energy it gives off as radiation at different frequencies. It is measured in terms of the radiant power emitted per unit area of the body, per unit solid angle the radiation is measured over, and per unit frequency. Planck showed that the following formula gives the spectral radiance of a blackbody at absolute temperature:

\[ B(\nu ,T) = \frac{2h\nu ^3}{c^2}\frac{1}{e^{\frac{h\nu}{k_B T}} – 1} \]

Where

B: Spectral radiance

ν: Wavelength of radiation

T: Absolute temperature

c: Speed of light

h: Planck’s constant

The spectral radiance can also be measured per unit wavelength instead of unit frequency. In this case, the equation gets modified to:

\[ B(\lambda ,T) = \frac{2hc^2}{\lambda^5}\frac{1}{e^{\frac{hc}{\lambda k_B T}} – 1} \]

The SI unit of B(ν, T) is W·sr⁻¹·m⁻²·Hz⁻¹, and that of B(λ, T) is W·sr⁻¹·m⁻³.

In the low-frequency limit, Planck’s law approximates to Rayleigh-Jeans law. In the high-frequency limit, Planck’s law approximates Wien’s law.

Planck’s law follows the distribution of energy according to Bose-Einstein statistics. The above expressions are obtained by multiplying the density of states in terms of frequency or wavelength with the photon energy and the Bose-Einstein distribution function with the normalization constant set to one.