Newton’s Second Law for Rotation

According to Newton’s second law for rotation,

Where,

τ: Torque

I: Moment of inertia

α: Angular acceleration

The above equation is critical in rotational kinematics and tells us how torque, moment of inertia, and angular acceleration are related.

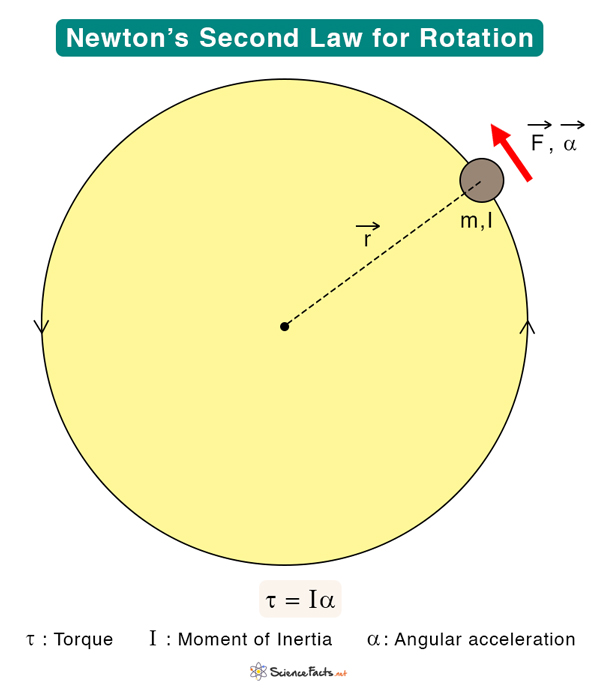
Consider an object of mass m rotates about an axis such that it executes a circular motion with radius r, as shown in the image. Let F be the force acting on it at any instant, resulting in a linear acceleration a. The following is the well-known version of Newton’s second law.

The magnitude of linear acceleration in the direction of the force is

The following equation relates the object’s tangential acceleration α to the linear acceleration.

Substituting this into Newton’s second law, we obtain

Multiplying both sides by r

The left-hand side of the above equation is the torque τ, where r is the lever arm and F is the force perpendicular to r. Also, for a point particle, the moment of inertia is given by the following expression.

Therefore, the applied torque on the object executing circular motion is

If a rigid body experiences several torques, the net torque is the sum of all the torques, which equals the moment of inertia times the angular acceleration.

The term Iα is scalar whose sign depends on whether the rotation is clockwise or counterclockwise.

In vector form, Newton’s second law for rotation is given by