Kinetic Theory of Gases
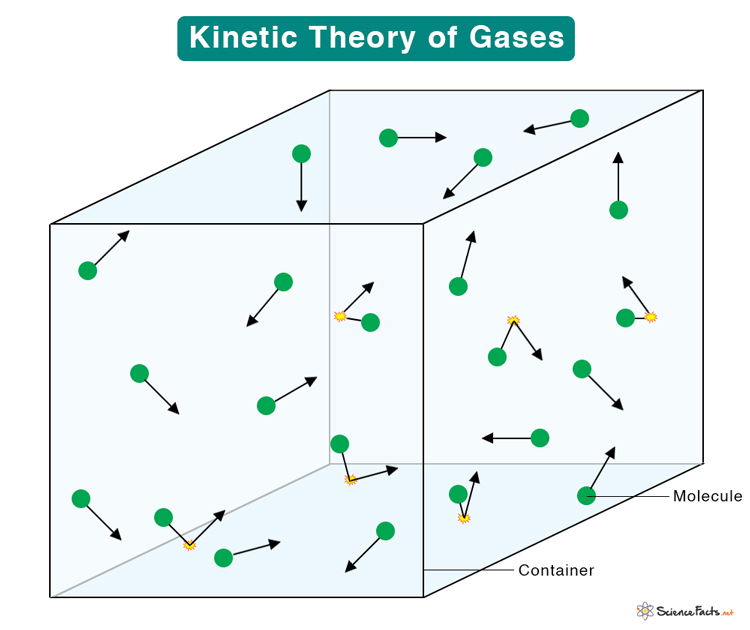
The kinetic theory of gases, also known as the kinetic molecular theory of gases, is based on the idea that a gas consists of a large agglomerate of tiny particles. The particles are separated by large distances and move randomly inside a container. Their rapid movement leads to collision among themselves and with the walls of the container.
The kinetic theory is a physical model to study the microscopic behavior of particles and their interactions. It can explain the macroscopic properties of gases, such as pressure, volume, and temperature (heat), and transport properties like thermal conductivity, viscosity, diffusivity, and Brownian motion. The consequence of the kinetic theory is that it helps to understand the correlation between the macroscopic properties and the microscopic phenomenon.
Several scientists developed the kinetic theory. Swiss mathematician and physicist Daniele Bernoulli laid the basis in his book Hydrodynamica in 1738.
Postulates
The kinetic molecular theory states that
- A gas is composed of many molecules that are treated as point particles. The molecules move randomly at a wide range of speeds.
- The distance of separation between the molecules is significant compared to the dimensions of the molecules. In other words, the volume occupied by the molecules is very insignificant compared to the volume of the gas.
- The molecules exert no electrostatic forces amongst themselves nor with the walls of the container.
- The molecules in constant random motion obey Newton’s laws. It means that a molecule moving in a straight line will continue to move unobstructed until it collides with another molecule or strike the wall.
- Collisions among molecules are perfectly elastic, which means that the molecules are perfect hard spheres.
- The average kinetic energy of the molecules is directly proportional to the absolute temperature.
According to kinetic molecular theory, most of the volume occupied by a gas is empty. Hence, gas has a low density. Density is the critical feature distinguishing a gas from liquid and solid, where molecules are so tightly packed that they are constantly in contact. Besides, unlike solid and liquid, gas can expand or contract easily.
All real gases behave like ideal gases at low pressures and high temperatures. At low pressures and high temperatures, the attractive forces among the molecules are negligible.
Kinetic Theory and Macroscopic Properties
All molecules possess standard physical properties like mass, momentum, and energy. The observable macroscopic properties like density, pressure, and temperature can be calculated from these properties. Since the number of molecules is large, it is impossible to study their behavior individually. For this reason, statistical methods are applied to analyze the properties of the gas as a whole. Kinetic molecular theory can explain the following properties:
Density (ρ): It is the sum of all the molecular masses (M) divided by the volume (V).
Pressure (P): Gas pressure arises due to molecules colliding with the walls of the container. As they collide with the walls of a container, the molecules impart momentum to the walls, resulting in a force perpendicular to the wall. We know that force is the change in momentum (m∆v), which when divided by area A, gives the pressure P.
Temperature (T): It represents the molecules’ mean kinetic energy (K.E.). As the molecules move, they possess kinetic energy, given by half of the mass (m) times velocity (v) squared. The higher the temperature, the higher the kinetic energy.
Kinetic Molecular Theory and Gas Laws
The kinetic theory of gases is noteworthy because the above assumptions lead to essential gas laws. These gas laws are a set of equations that relates the pressure (P), volume (V), and temperature (T). The ideal gas law relates the above three in terms of the universal gas constant (R) and the number of moles (n).
1. Boyle’s Law
Boyle’s law states that the pressure of a gas is inversely proportional to its volume, provided the temperature is constant. The pressure depends on the number of times per second that the molecules strike the walls of the container. If the gas is compressed to a smaller volume, the same number of molecules is now acting against a smaller surface area. As a result, the number striking per unit area, or the pressure, is now higher.
2. Charles’ Law
Charles’s law states that the volume occupied by a gas is directly proportional to the temperature as long as the pressure is constant. Increasing the temperature raises the average kinetic energy of the molecules. If the molecules move rapidly, they will strike the walls more forcefully. Hence, the pressure will increase. However, the area where the molecules strike must also increase to compensate for the pressure. As the area increases, the volume also increases.
3. Avogadro’s Law
Avogadro’s law states that equal volumes of all gases contain an equal number of molecules under the same temperature and pressure conditions. Increasing the number of gas molecules in a closed container increases the number of collisions with the wall. The pressure will increase. In order to keep the pressure constant, the volume must increase and create a larger surface so that molecules hit the wall infrequently.
4. Amonton’s Law
Amonton’s law states that the pressure exerted by a gas is directly proportional to the temperature as long as the volume is constant. The average kinetic energy of a gas molecule depends only on the temperature of the gas. Thus, the average kinetic energy of the gas particles increases as the gas becomes warmer. An increase in average kinetic energy means an increase in average molecular velocity. The faster these particles move just before hitting the wall, the greater the force they exert on the wall. Since the force per collision increases as the temperature rises and the volume remains constant, the pressure of the gas must increase as well.
Kinetic Molecular Theory and Root Mean Squared Speed
As mentioned before, the gas molecules are in constant random motion. The kinetic energy of a molecule of mass m and moving with a velocity v is given by the following expression:
The individual molecules have a wide range of energies because of the speed distribution that arises from the collisions between the gas molecules. Although these collisions are elastic with no loss in kinetic energy, the individual speed may change. However, the average kinetic energy of the molecules remains the same. The average energy associated with the molecular motion is based on Boltzmann’s statistical distribution function.
Maxwell and Boltzmann studied the kinetic behavior of gases and came up with the idea of speed distribution. They found that the speed of gaseous molecules ranges from zero to infinity. Hence, a reasonable method to estimate their speed was to calculate the root mean square speed.
According to the kinetic theory, the average kinetic energy of the gas molecules is proportional to the absolute temperature.
Where
Eavg : Average kinetic energy
T : Absolute temperature
k : Boltzmann’s constant
We can get the root mean square (rms) speed (vrms) by combining this equation with the kinetic energy equation.
It is easier to calculate vrms from the molar mass of a gas. Therefore, we multiply the numerator and the denominator of the term 3kT/m by Avogadro’s number (NA).
Where
R (= kNA) : Universal gas constant
M (= mNA) : Molar mass of the gas
This equation tells us that the rms speed of the gas molecules is inversely proportional to the square root of the molar mass. For two gases with different molar masses, the heavier one will have a slower speed.
Example Problem 1: Calculate the rms speed of oxygen molecules at 27 ˚C. (Molar mass of oxygen = 16 g/mol , R = 8.34 J/mol·K)
Solution:
Given
M = 16 g = 16 x 10-3 kg
T = 273 + 27 = 300 K
R = 8.314 J/mol·K
-
References
Article was last reviewed on Friday, February 17, 2023





This is quite informative. I strongly recommend your services to all science teachers.