Inelastic Collision

What is Inelastic Collision

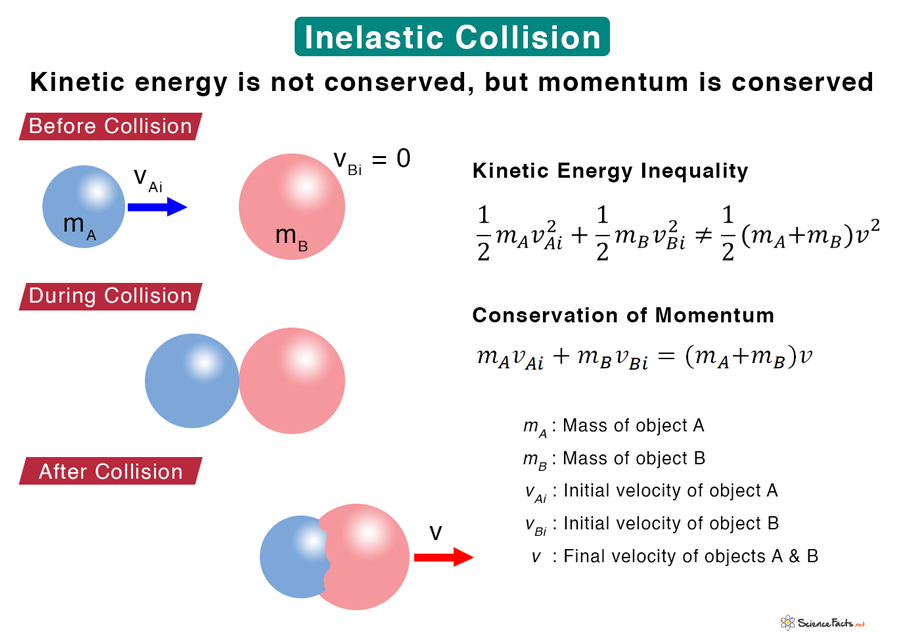
An inelastic collision is a collision in which the kinetic energy of the colliding objects is not conserved. In other words, the total kinetic energy before the collision is not equal to the total kinetic energy after the collision. It is converted into dissipative energy like sound, heat, or friction. For example, when a tennis ball is released from a height, it bounces to a lower height. The reason is that some of its kinetic energy is lost due to sound and friction with the ground.

A perfectly inelastic collision, also known as a completely inelastic collision, loses the maximum amount of kinetic energy. In such a situation, objects stick together after the collision. For example, when a ball made out of mud is thrown at a wall, it sticks to it. In an inelastic collision, momentum is conserved. It means that the total momentum before the collision is the same as after.

Characteristics and Properties

In an inelastic collision:

Total momentum remains the same before and after the collision
Total kinetic energy does not remain the same before and after collision
Kinetic energy is lost due to dissipative factors like sound, friction, and heat
Objects may deform or dent or even stick together

Examples

Dropping clay ball: When a clay ball is dropped, it does not bounce. Instead, it sticks to the ground.
Car crash: When two cars collide, they deform and change speed and direction. When a car hits a tree or lamppost, it comes to a stop.
Ballistic pendulum: It is a device used to measure a bullet’s momentum. The bullet collides with a pendulum and is embedded in a block. After the collision, the bullet and the block swing together.

Equations

Suppose an object of mass m_A moving with velocity v_A collides with another object with mass m_B moving with velocity v_B. The two objects stick together after the collision and move with a common velocity v. From conservation of momentum, we have

\[ m_Av_A + m_Bv_B = (m_A + m_B) v\\ v = \frac{m_Av_A + m_Bv_B}{m_A+m_B} \]

The above equation gives the common velocity of the objects after the inelastic collision.

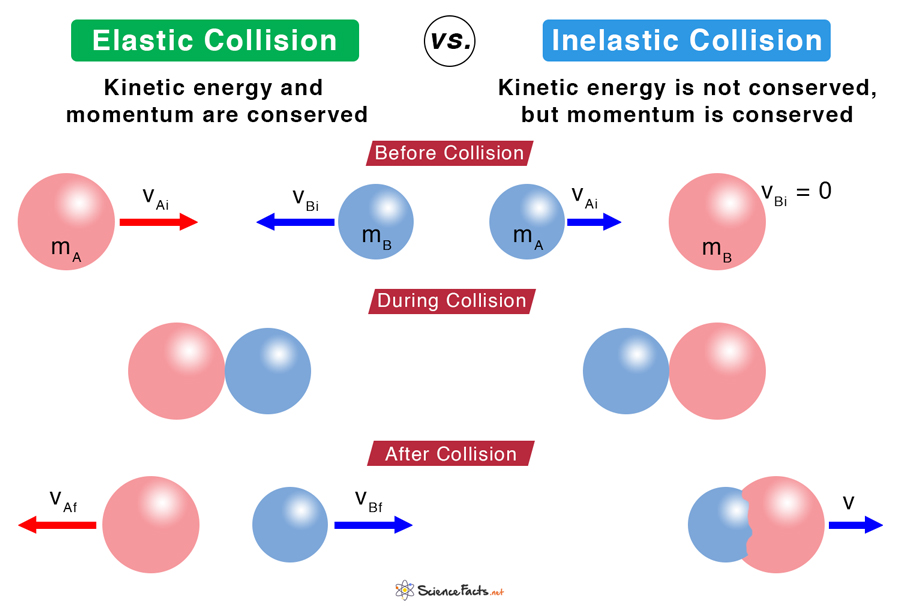
Elastic and Inelastic Collisions

Both elastic and inelastic collisions are types of collisions that conserve momentum. The following table gives the differences between the two.

	Elastic Collision	Inelastic Collision
Definition	A collision where momentum and kinetic energy are conserved	A collision where momentum is conserved, but kinetic energy is not conserved
Kinetic Energy	It remains the same before and after the collision	It does not remain the same before and after the collision. Some energy is lost due to sound, heat, and friction
Physical change	Highly unlikely	Most collisions result in deformation or dent
Examples	Newton’s cradle and collision between atoms	Ballistic pendulum and collision between cars

Coefficient of Restitution

The coefficient of restitution (C_R) is the ratio between the final and the initial velocities of an object undergoing collision. It takes a value between 0 and 1, with 0 meaning a perfectly inelastic collision and 1 being perfectly elastic. The following equation gives the value.

\[ C_R = \frac{v_f}{v_i} \]

The coefficient of restitution of a golf ball on a steel surface is 0.9, and a billiard ball can be up to 0.98.

Problems and Solutions

Problem: A 2500 kg truck traveling at 60 km/hr strikes a stationary 1500 kg car, locking the two vehicles together.

a) What is the final velocity of the two vehicles in m/s?

b) How much of the initial kinetic energy is lost to the collision?

Solution:

Given,

m_A = 2500 kg

m_B = 1500 kg

v_A = 60 km/hr = 60 km x 1000 m/km/(1 hr x 3600 s/hr) = 16.67 m/s

v_B = 0

a) The combined velocity is given by,

v = (m_Av_A + m_Bv_B)/(m_A + m_B)

Or, v = (2500 kg x 16.67 m/s + 1500 kg x 0)/(2500 kg + 1500 kg)

Or, v = 10.42 m/s

b) Kinetic energy before collision

(K.E.)_i = ½ m_Av_A² + ½ m_Bv_B² = ½ x 2500 kg x (16.67 m/s)² + 0 = 347361 J

Kinetic energy after collision

(K.E.)_f = ½ (m_A+ m_B)v² = ½ x (2500 kg + 1500 kg) x (16.67 m/s)²= 217152 J

Therefore, fraction of energy lost is

1 – (K.E.)_f/(K.E.)_I = 217152 J/347361 J = 0.38

FAQs

Q.1. What type of collision is an explosion?

Ans. An explosion is a perfectly inelastic collision which is reversed. Here, momentum is conserved, but the kinetic energy increases.

References
- 1. What are elastic and inelastic collisions? – Khanacademy.org
  2. Inelastic Collision – Hyperphysics.phy-astr.gsu.edu
  3. Perfectly Inelastic Collision – Thoughtco.com
  4. Inelastic Collision – Courses.lumenlearning.com
  5. Inelastic Collision – Batesville.k12.in.us
  6. Inelastic collision in One Dimension – Pressbooks.bccampus.ca