Hooke’s Law
What is Hooke’s Law
Hooke’s Law states that for small displacements or deformations, the applied force is directly proportional to the displacement. Hooke’s Law helps explain the mechanical properties and strength of elastic materials.
This law is named after the British physicist Robert Hooke, who first formulated the relationship between force and displacement in 1660 and published it in 1678.
Mathematical Form of Hooke’s Law
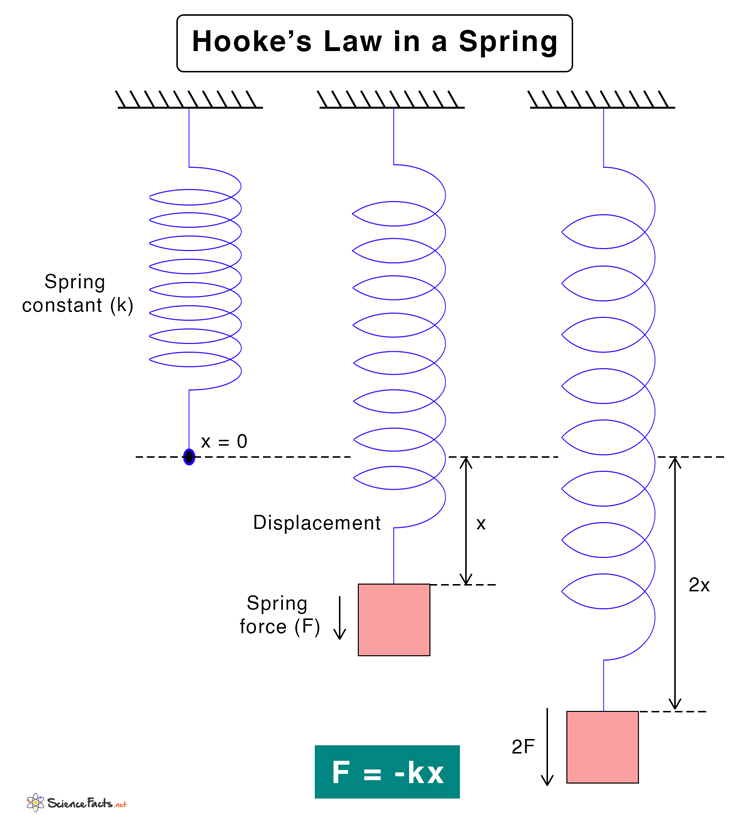
Example: Spring
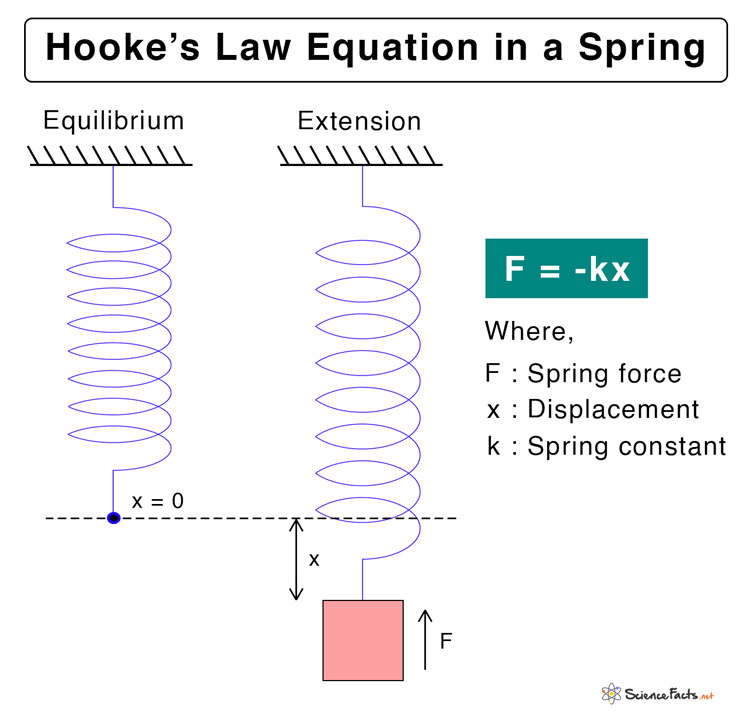
Hooke’s Law describes the forces acting on a spring. A spring at rest is in its equilibrium position. When a force is applied to compress or extend it, the spring will restore its initial position. The force with which it restores is known as spring force and can be quantified using Hooke’s law, which states that the restoring force F is proportional to the spring’s displacement x.
F ∝ x
Or, F = -kx
Where k is termed as the force constant or spring constant.
The negative sign is because the restoring force is in the opposite direction to the displacement. It is responsible for bringing back the spring to its equilibrium position. This equation applies to both compression and extension of spring. The spring force can be measured using a spring tester or a weighing scale.
The SI unit of force in Hooke’s Law is the Newton (N), where 1 N = 1 kg·m/s².
Spring Constant
The spring constant is defined as,
k = F/x
Suppose F = 1 N and x = 1 m, then
k = 1 N/ 1 m = 1 N/m
Therefore, the spring constant is defined as the force required to displace the spring by one meter. It has a unit of Newton per meter (N/m) and a dimension given by MT-2.
Elastic Energy
When a spring is stretched or compressed, work is done on it. The work done on a spring is stored as elastic potential energy. As the deformation is removed, energy is released, and the potential energy is converted into kinetic energy. The work done W in compressing or extending the spring by a distance x is given by,
W = ΔPE = ½kx2
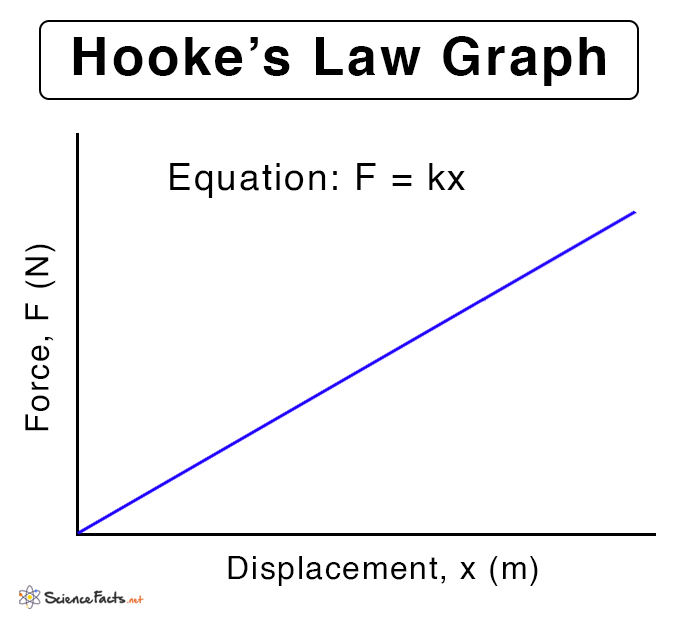
Hooke’s Law Graph
Hooke’s law can be expressed graphically in which force is plotted against displacement. Since force and displacement are directly proportional, the graph of force vs. displacement is a straight line with a slope equal to the spring constant (k).
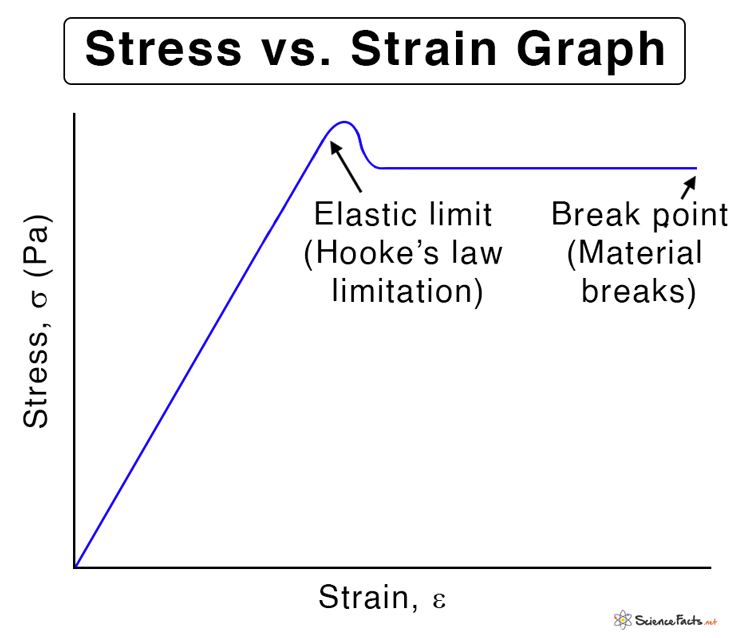
Hooke’s Law in Elasticity
Elasticity is the property of an object that allows it to resist deformation and return to its original shape. Hooke’s Law can be applied to elasticity as long as the deformation is within the ‘elastic limit’. However, we need to understand two fundamental concepts: stress and strain.
Consider any object that is subjected to an applied force resulting in deformation. Stress quantifies the applied force. It is defined as the force applied per area of the object. Strain describes the deformation. It is defined as the ratio of change in length (or volume) to the object’s original length (or volume). Hooke’s Law establishes a relationship between stress and strain.
Stress-Strain Equations
An object can be deformed in different ways, resulting in three types of stress and strain. They are longitudinal or normal, volumetric, and shear. For each type, Hooke’s law can be written as follows:
1. Longitudinal or Normal
σ = E x ε
Where,
σ is the longitudinal or normal stress
ε is the longitudinal or normal strain
E is Young’s modulus
2. Shear
τ = G x γ
Where,
τ is the shear stress
ϒ is the shear strain
G is the shear modulus
3. Volumetric
∆P = – K x (∆V/V0)
Where,
∆P is the pressure change
∆V is the volume change
V0 is the original volume
K is the bulk modulus
The negative sign implies the fact that an increase in pressure reduces the volume.
Applications of Hooke’s Law
Hooke’s law can be applied to many devices like a mechanical clock, spring balances, watches, and manometers (pressure gauges). It has found its uses in various disciplines like acoustics, seismology, molecular mechanics, engineering, and construction.
Limitations of Hooke’s Law
Hooke’s law is applied to a limited deformation known as the elastic limit. If an object is stretched beyond its elastic limit, it will not return to its original shape and will undergo permanent deformation.
Solved Examples and Problems
Problem 1. How much force is needed to pull a spring with a spring constant of 15 N/m to a distance of 15 cm?
Solution
Given,
k = 15 N/m
x = 15 cm = 0.15 m
Formula: F = kx
Therefore,
F = 15 N/m x 0.15 m = 2.25 N
Problem 2. A spring is pulled to 12 cm and held in place with a force of 550 N. What is its spring constant?
Solution
Given,
F = 550 N
x = 12 cm = 0.12 m
Formula: F = kx
Therefore,
k = F/x
or, k = 550 N/0.12 m = 4583 N/m
Problem 3. What is the force required to stretch a 15 cm-long spring, with a spring constant of 80 N/m, to a length of 17 cm?
Solution
Given,
l1 = 15 cm
l2 = 17 cm
k = 80 N/m
Therefore,
x = l2 – l1 = 17 cm – 15 cm = 2 cm = 0.02 m
From Hooke’s law equation,
F = kx
F = 80 N/m x 0.02 m = 1.6 N
Problem 4. What is the spring constant of a spring that needs a force of 4 N to compress from 50 cm to 45 cm?
Solution
Given,
F = 4 N
l2 = 50 cm
l1 = 45 cm
Therefore,
x = l2 – l1 = 45 cm – 50 cm = – 5 cm = – 0.05 m
or, |x| = 0.05 m
From Hooke’s law equation,
F = kx
or, k = F/x = 4N / 0.05 m = 80 N/m
FAQ
Ans. The generalized Hooke’s law is used to predict the deformations in a material caused by an arbitrary combination of stresses.
Ans. Although it is an elastic material, rubber bands generally do not follow Hooke’s law.
Ans. Yes, Hooke’s Law is considered valid for shearing stress and strain as long as the shearing stress remains within the elastic limit of the material.
-
References
Article was last reviewed on Friday, February 14, 2025







Thank you so much for sharing i have learnt some thing which i don’t know please keep sharing.