Escape Velocity

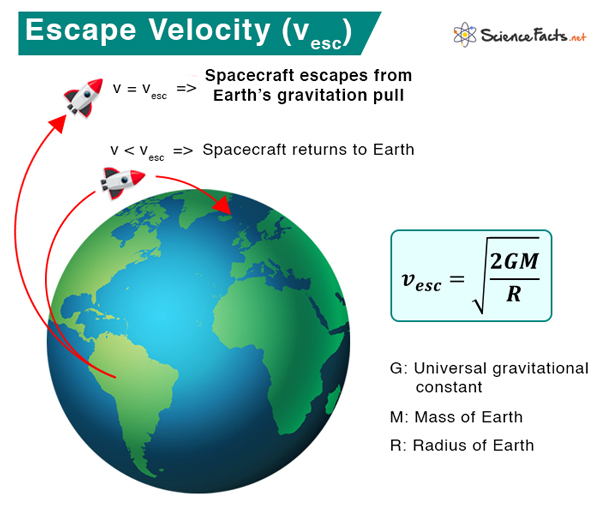
If you throw an object straight up, it will rise until gravity stops it and returns it to Earth. The force of gravity reduces as the distance from the center of the Earth increases. However, suppose you can throw the object with enough initial upward velocity so that decreasing force of gravity does not completely slow it to a complete stop. In that case, the velocity can always be high enough to overcome the Earth’s gravitational force. The initial velocity required to attain that situation is called escape velocity.

Escape velocity is the speed required for an object to be projected to overcome the Earth’s gravitational force. The object escapes from Earth’s surface into space without ever falling back.

Formula

The equation for escape velocity is as follows:

\[ v_{esc} = \sqrt{\frac{2GM}{R}} \]

Where

v_esc is the escape velocity

G is the universal gravitational constant (= 6.67 x 10^-11 m³ ˑ kg^-1ˑ s^-1)

M is the mass of the earth (= 5.972 x 10²⁴ kg)

R is the radius of the earth (= 6.371 x 10⁶ m)

Escape Velocity of Earth

The escape velocity on Earth’s surface is

\[ v_{Earth} = \sqrt{\frac{2 \times 6.67 \times 10^{-11} \hspace{0.1 cm} m^3 \cdot kg^{-1} \cdot s^{-2} \times 5.927 \times 10^{24} \hspace{0.1 cm} kg}{6.371 \times 10^6 \hspace{0.1 cm} m}} \\ v_{Earth} = 11182 \hspace{0.1 cm} m/s \hspace{0.1 cm} \text{or} \hspace{0.1 cm} 11.182 \hspace{0.1 cm} km/s \]

Therefore, the minimum velocity required to project an object from Earth’s surface to escape the gravitational pull is 11.182 km/s or 25,000 mph. Scientists use this value to send rockets into space.

Example Problem

If the mass of Mars is 6.41 x 10²³ kg and its radius is 3.39 x 10⁶ m, what is the escape velocity of an object launched from Mars?

Solution

Given

M_Mars= 6.41 x 10²³ kg

R_Mars = 3.39 x 10⁶ m

G = 6.67 x 10^-11 m³ ˑ kg^-1ˑ s^-1

The escape velocity from Mars is

\[ v_{Mars} = \sqrt{\frac{2GM_{Mars}}{R_{Mars}}} \\ => v_{Mars} = \sqrt{\frac{2 \times 6.67 \times 10^{-11} \hspace{0.1 cm} m^3 \cdot kg^{-1} \cdot s^{-2} \times 6.41 \times 10^{23} \hspace{0.1 cm} kg}{3.39 \times 10^6 \hspace{0.1 cm} m}} \\ v_{Mars} = 5022 \hspace{0.1 cm} m/s \hspace{0.1 cm} \text{or} \hspace{0.1 cm} 5.02 \hspace{0.1 cm} km/s \]

The following table lists the escape velocities of several planets, the sun, and the moon.

Planetary Body	Escape Velocity (km/s)
Earth	11.2
Mars	5.02
Jupiter	59.5
Mercury	4.3
Venus	10.36
Pluto	1.21
Sun	617
Moon	2.38

Derivation

We use the energy conservation principle to derive the expression for escape velocity. The kinetic energy of the object is

\[ \text{K.E.} = \frac{1}{2} mv^2 \]

Where m is the object’s mass and v is its velocity.

The gravitational potential energy on the surface of the earth is

\[ P.E. = \frac{GMm}{R} \]

From the law of conservation of energy, the kinetic energy comes from the gravitational potential energy.

\[ \frac{1}{2} m{v_{esc}}^2 = \frac{GMm}{R} \\ => v_{esc} = \sqrt{\frac{2GM}{R}} \]

In the escape velocity calculation, we assume no friction with the Earth’s atmosphere.

After achieving the escape velocity, the object does not require any impulse to escape from Earth’s gravitational field. The object achieves zero velocity asymptotically at an infinite distance from the Earth’s surface, never to return.