Elastic Collision
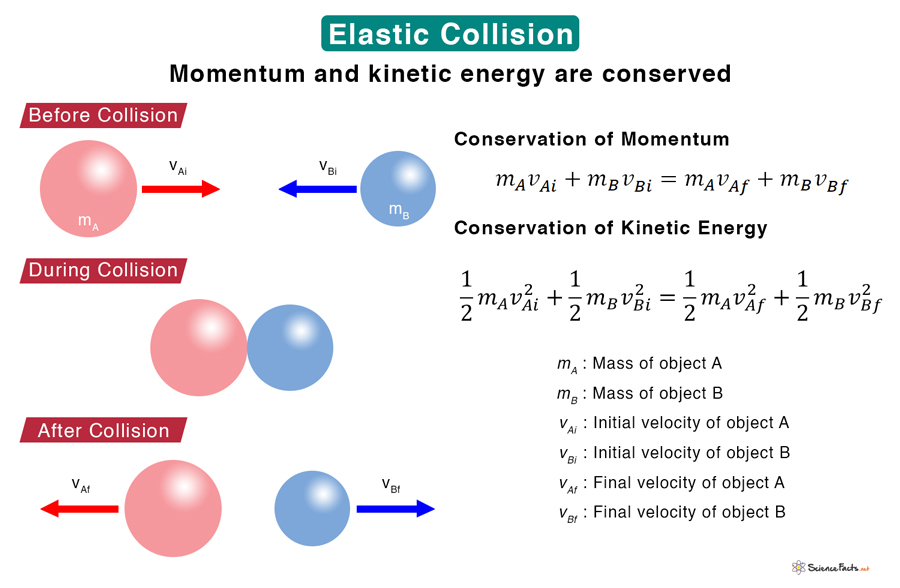
An elastic collision is a collision between two objects in which the momentum and kinetic energy are conserved. It means that the total momentum and the total kinetic energy of the objects remain the same before and after the collision. A perfectly elastic collision, also known as a completely elastic collision, assumes no dissipative forces like sound, friction, or heat. An example of a nearly perfect elastic collision is that between billiards balls. When two billiard balls collide, they rebound and move in different directions with velocities different from their initial values. If the kinetic energy is not conserved, the result is an inelastic collision.
Examples
- Newton’s cradle: It is a device that demonstrates elastic collision with swinging spheres.
- Rutherford scattering: The scattering between the alpha particles and the gold nuclei is elastic.
- Gravitational slingshot: Also known as a gravity assist, it uses the gravitational force of a planet to change the course of an approaching satellite.
Characteristics and Properties
In an elastic collision:
- Total kinetic energy before and after the collision remains unchanged
- Total momentum before and after the collision remains unchanged
- Energy is not dissipated through heat or friction
- Colliding objects do not deform
Equations
Suppose two objects, A and B, with masses mA and mB traveling with velocities vAi and vBi collide head-on. After the collision, the objects change direction and velocity. Let vAf and vBf be the final velocities, which we are interested in calculating.
Applying the law of conservation of momentum,
Applying the law of conservation of kinetic energy,
As there are two equations and two unknowns, we use the method of simultaneous equations to solve for vAf and vBf.
These equations give the final velocities of objects A and B after a head-on collision. Let us look at a few specific cases.
Case 1: Object A is at rest, and object B is in motion.
Here, vAi = 0. Therefore,
Case 2: Object B is at rest, and object A is in motion.
Here, vBi = 0. Therefore,
Case 3: Objects A and B have the same mass.
Here, mA = mB = m
According to the equations, the two objects bounce off each other, exchanging velocities. So, if two objects of equal masses collide head-on, they exchange momentum.
Now, suppose B is at rest (vBi = 0). Then,
It means that A comes to a stop, and B picks up the same speed as A.
Problems and Solutions
Problem 1: Two bumper cars, A and B, at an amusement park collide elastically as one approaches the other directly from the rear. Car A, in front, has a mass of 650 kg. Car B, behind, has a mass of 550 kg. The car in front was traveling at 4.30 m/s while the car behind hit him with a velocity of 5.70 m/s. What are their final velocities after the collision?
Solution:
Given,
mA = 650 kg, mB = 550 kg, vAi = 4.3 m/s, and vBi = 5.7 m/s
We have,
vAf = (mA – mB)/(mA + mB) vAi + 2mB/(mA + mB) vBi
vAf = (650 kg – 550 kg)/(650 kg + 550 kg) x 4.3 m/s + 2 x 550 kg/(650 kg + 550 kg) x 5.7 m/s
Or, vAf = 5.58 m/s
And,
vBf = 2mA/(mA + mB) vAi – (mA – mB)/(mA + mB) vBi
Or, vBf = 2 x 650 kg/(650 kg + 550 kg) x 4.3 m/s – (650 kg – 550 kg)/(650 kg + 550 kg) x 5.7 m/s
Or, vBf = 4.18 m/s
Problem 2: Calculate the velocities of two objects, A and B, following an elastic collision, given that mA = 1.75 kg, mB = 3.25 kg, vA = 6.00 m/s, and vB = 0.
Solution:
Given,
mA = 1.75 kg, mB = 3.25 kg, vA = 6.00 m/s, and vB = 0.
Here, object A is moving, and object B is at rest (vBi = 0). Therefore,
vAf = (mA – mB)/(mA + mB) vAi
Or, vAf = (1.75 kg – 3.25 kg)/(1.75kg + 3.25 kg) x 6 m/s
Or, vAf = – 1.8 m/s
And,
vBf = 2mA/(mA + mB) vAi
Or, vBf = 2 x 1.75 kg/(1.75 kg + 3.25 kg) x 6 m/s
Or, vBf = 4.2 m/s
The negative sign indicates that object A bounces and move in the opposite direction after the collision.
-
References
Article was last reviewed on Thursday, April 6, 2023









The equation for kinetic energy in the graphic is wrong. You have 1/2mBf * VAf^2 instead of 1/2mAf * VAf^2
Thank you. We will make the correction.
Good luck