Capillary Action
Capillary action is a phenomenon in which liquid flows through a narrow tube without the assistance of any force. It refers to the ascension of liquid through a capillary tube due to forces of adhesion and cohesion and, typically, against gravity. Capillary action occurs when the force of adhesion is greater than the force of cohesion.
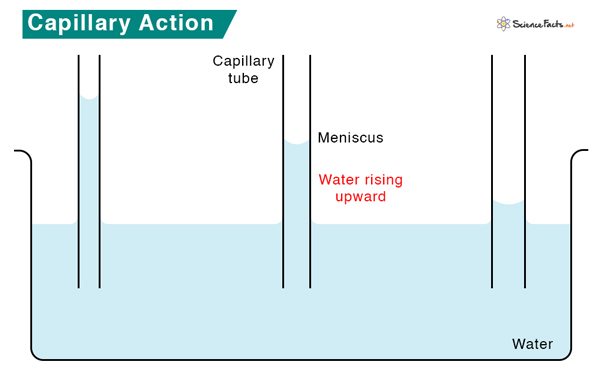
For instance, capillary action is observed when placing a thin straw into a cup of water. Water goes into the straw and rises higher than the surrounding water in the cup. The water inside the straw works against gravity, which would questionably pull it down.
How Does Capillary Action Work
The two properties that make capillary action possible are:
Cohesive Force – Force due to intermolecular attractions between molecules of the same kind, that is, liquid molecules. Cohesive force leads to surface tension in which the surface molecules bond and form an impenetrable layer.
Adhesive Force – Force due to intermolecular attractions between molecules of different kinds, that is, between the liquid and the material of the capillary tube.
The combination of cohesive and adhesive forces causes capillary action. However, it does not occur in all liquids. For instance, mercury will not rise in a narrow tube because its cohesive force is stronger than the adhesive force. At 20 oC, mercury’s surface tension is 486 dyne/cm, much higher than water’s (72.8 dyne/cm).
Examples
Capillary action is observed in real life through various examples.
- Plaster and paper towels uptake water since both are porous materials with a strong affinity toward water.
- When a candle burns, the heat from the flame melts the wax. The melted wax traverses up the wick, supplying the fuel necessary to sustain the burning.
- A phenomenon known as thin-layer chromatography separates dyes used in the food industry using capillary action.
- Capillary action occurs naturally in our eyes. It pumps out the tear fluid from our eyes and removes dirt and dust particles.
Capillary Action of Water
Capillary action is a property of water. Water molecules are both cohesive and adhesive because of their polarity. This cohesive property makes water molecules bond firmly, producing high surface tension. The adhesive property allows the molecules to adhere to the walls of the tube, typically made of glass. Adhesion of water to glass causes an upward force on it at the edge, raising the water level in the tube and resulting in an upward meniscus, as shown in the image above.
Capillary Action in Plants
In biology, plants use capillary action to bring water from the soil and distribute it to their various parts. Water contains essential nutrients that are responsible for plants’ growth. As we have seen that capillary action occurs in a capillary tube, plants have narrow tubes called xylem tissue.
As they exit the root system, the water molecules stick together and to the side walls of the xylem tissue. This process is known as transpiration pull. Transpiration is responsible for tall towering trees to supply water to the top leaves from the roots through stems and branches.
Plants extract water exclusively from their roots and transport it to its entirety. Without capillary action, they will not be able to survive.
Height of Liquid Column
A liquid rises inside a thin cylindrical tube due to capillary action. It is possible to determine the height, h, of the liquid column. The following formula gives the height to which the liquid rises.
Where
θ is the contact angle
ρ is the density of the liquid
g is the acceleration due to gravity
r is the radius of the tube in which the liquid is confined
We can use the values at 20 0C and reduce the above equation. For water confined to a glass tube of radius r, we have
θ = 200
ρ = 998 kg/m3
g = 9.8 m/s2
Plugging in these values, we get
Therefore, the tube needs to be sufficiently small in diameter for capillary action to occur.
-
References
Article was last reviewed on Friday, July 28, 2023







