Bravais Lattice

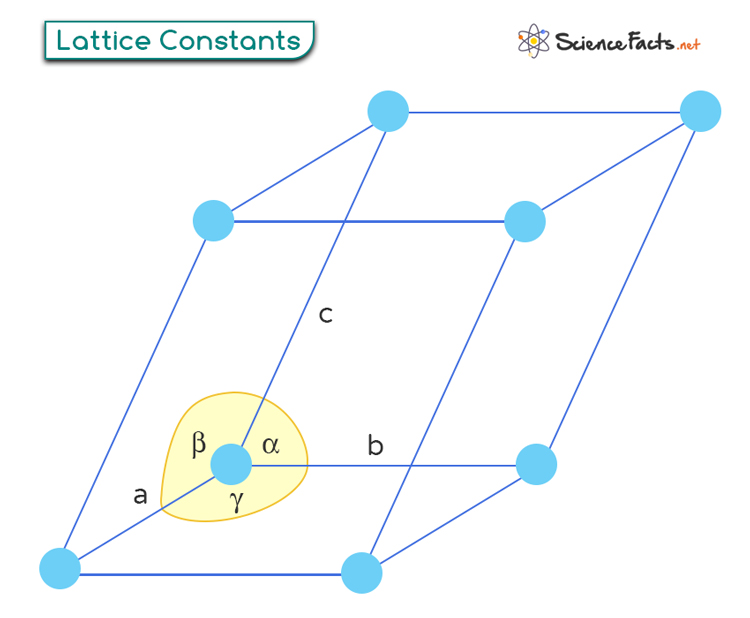
The lattice constants are characteristic length scales associated with the lattice. It represents the distance between adjacent lattice points. Within each Bravais lattice, a repeating unit called the unit cell exists. The unit cell is the smallest repeating structure representing the entire crystal lattice.

Lattice constants define the size and shape of a unit cell. They refer to the lengths of the edges of a unit cell. They are typically denoted by letters “a”, “b”, and “c” for the three dimensions in a crystal lattice. The significance of lattice constants lies in their relationship, which is unique for each Bravais lattice.

Lattice constants also provide information about the angles between different edges or axes within a crystal structure. These angles are known as interaxial angles and are denoted by “α”, “β”, and “γ”. The values of the lengths and angles determine the overall dimensions and symmetry of the crystal structure.

There are 14 types of Bravais lattices, classified into seven crystal systems (cubic, tetragonal, orthorhombic, trigonal (rhombohedral), monoclinic, triclinic, and hexagonal). Each crystal system has one or more types of Bravais lattices associated with it. Also, each crystal system is defined by a unique set of lattice constant relationships.

1. Cubic

A cubic crystal is characterized by a cubic unit cell, which means that all three edges of the unit cell are of equal length and have 90^∘ angles between them.

Cubic crystals exhibit a high degree of symmetry. They come in three types:

i. Simple Cubic (SC) Crystal: In a simple cubic crystal, also known as primitive cubic, each lattice point is located at the corners of the cube. SC structures are rare but can be found in certain elements, such as polonium.

ii. Body-centered Cubic (BCC): In a body-centered cubic crystal, in addition to the lattice points at the corners of the cube, there is one lattice point located at the center of the cube. BCC structures can be observed in metals like iron, chromium, and tungsten.

iii. Face-Centered Cubic (FCC) Crystal: In a face-centered cubic crystal, lattice points are located not only at the corners of the cube but also at the centers of each face of the cube. FCC structures are commonly found in aluminum, copper, and gold.

2. Tetragonal

A tetragonal crystal has a rectangular prism-shaped unit cell. It is characterized by three mutually perpendicular axes, two of which are equal in length and the third of a different length. The angles between the axes are all 90^∘.

There are two types of tetragonal lattices:

i. Primitive Tetragonal Lattice: In this type, lattice points are located only at the corners of the unit cell, similar to a simple cubic lattice.

ii. Body-Centered Tetragonal Lattice: In this type, lattice points are located at the corners and center of the unit cell. This is analogous to a body-centered cubic lattice but with unequal axis lengths.

Materials exhibiting a tetragonal lattice structure can be found in various substances, from metals like zirconium and titanium to minerals like rutile and cassiterite.

3. Orthorhombic

An orthorhombic crystal is characterized by three mutually perpendicular axes of different lengths. The angles between these axes are all 90^∘, leading to a rectangular or parallelepiped-shaped unit cell.

There are four types of orthorhombic crystal structures:

i. Primitive Orthorhombic: In a primitive orthorhombic structure, also known as simple orthorhombic, the lattice points are located only at the corners of the unit cell.

ii. Body-Centered Orthorhombic: In a body-centered orthorhombic structure, there is an additional lattice point at the center of the unit cell in addition to the lattice points at the corners.

iii. Face-centered Orthorhombic: In a face-centered orthorhombic structure, lattice points are present not only at the corners of the unit cell but also at the centers of each face of the unit cell.

iv. Base-Centered Orthorhombic: In this type of structure, in addition to lattice points at the corners of the unit cell, there is an additional lattice point at the center of one or more of the faces of the unit cell.

Orthorhombic crystals can be found in numerous mineral formations, such as the stunning topaz and the shimmering aragonite.

4. Rhombohedral

A rhombohedral crystal forms a structure with rhombohedron unit cells. It is characterized by axes of equal length and non-orthogonal angles between them.

5. Monoclinic

A monoclinic crystal is characterized by three axes of unequal lengths. Two pairs of axes are perpendicular, while the third pair makes an angle that is not 90^∘. This results in a parallelepiped unit cell.

There are two types of Bravais lattices in the monoclinic system:

i. Simple (Primitive) Monoclinic: Like the primitive orthorhombic lattice, the primitive monoclinic lattice has lattice points at the corners of the parallelepiped.

ii. Base-centered Monoclinic: In addition to the corner lattice points, additional lattice points are located at the center of the two bases of the unit cell.

Monoclinic crystals can be found in minerals such as gypsum, orthoclase feldspar, and clinopyroxene.

6. Triclinic

The triclinic lattice structure has three unequal axes and angles that are not right angles. It is the least symmetrical among all the crystal systems. There can be only one type of triclinic Bravais lattice, which is a primitive cell.

Minerals like microcline, plagioclase, and labradorite exhibit triclinic symmetry, showcasing the diverse nature of crystalline structures found in nature.

7. Hexagonal

The hexagonal lattice can be described by a right rhombic prism unit cell. Two of its axes are equal and make an angle of 120^∘. A third axis is perpendicular, defines the height of the hexagon, and is perpendicular to the two base axes. A simple hexagonal cell has relations, as shown in the image below.

Graphite is an example of a crystal that crystallizes in the hexagonal crystal system.

In addition to the hexagonal lattice, there exists another structure known as the hexagonal closed-packing (HCP) structure. The HCP structure is like a stack of layers alternating between two types: A and B. In layer B, atoms fit snugly into the spaces left by the atoms in layer A, making everything fit tightly together. This tight arrangement is super efficient for packing atoms closely. Overall, this stacking creates a repeating pattern that looks like a hexagon when viewed from the top, and it forms a structure that is tightly packed both horizontally and vertically.