Ampere’s Law

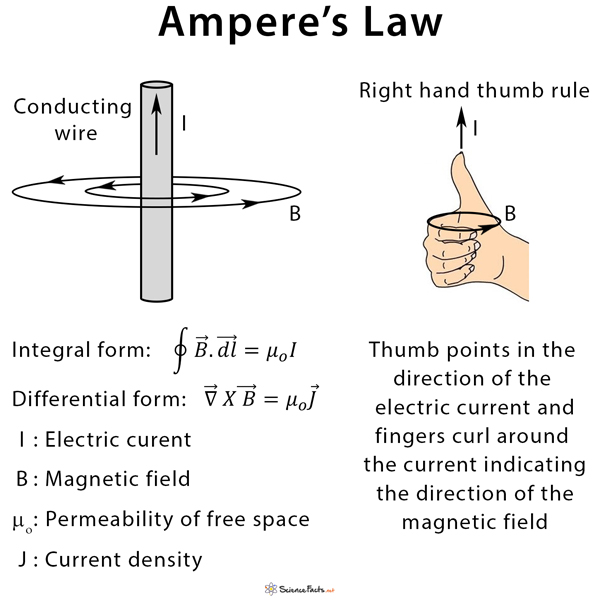
Ampere’s law, or Ampere’s circuital law, is a mathematical statement used in electromagnetism that gives a relationship between a current and the magnetic field it generates. The magnetic field produced by an electric current is proportional to the magnitude of the current with a proportionality constant equal to the permeability of free space (μ_o), a universal constant in physics. Its value is 4π X 10^-7 H/m. In its discrete form, Ampere’s law states that for any closed path (Amperian loop), the sum of the length elements times the magnetic field in the direction of the length element is equal to the permeability times the electric current enclosed in the loop. Ampere’s law can be expressed in both integral and differential forms. The integral form is generally used to determine the magnetic field. This magnetic field, if derived from Biot-Savart law, will yield the same result.

Ampere’s law has been named after French physicist and mathematician André-Marie Ampère. However, it was Scottish mathematical physicist James Clerk Maxwell who derived in 1861 it after performing experiments with current-carrying currents.

The Biot-Savart’s Law can be utilized to calculate the magnetic field due to a current-carrying wire, from which Ampere’s law can be derived.

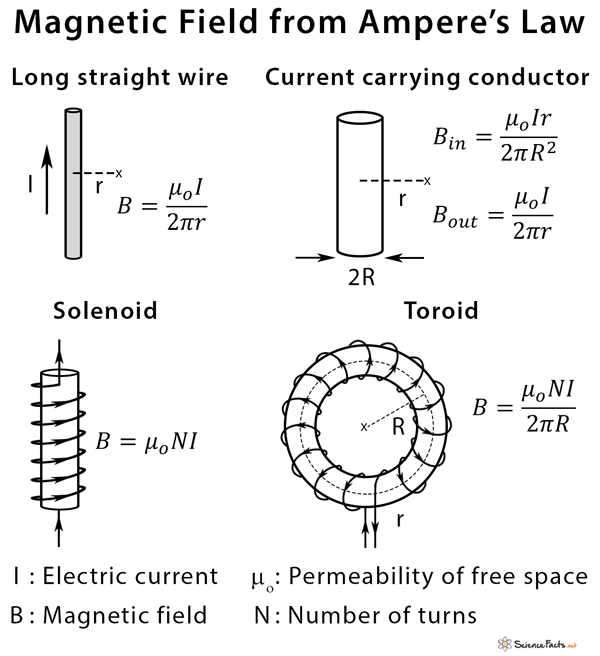
The integral form of Ampere’s law is used to determine the magnetic field since it can be integrated over in space. Hence, it is used to find the fields generated by devices like a long straight conducting wire, coaxial cable, cylindrical conductor, solenoid, and toroid. Usually, the right-hand thumb rule is applied to find the direction of the magnetic field.

Ampere’s law has many practical applications. The primary usage is, of course, calculating the magnetic field generated by an electric current. This law is useful in electromagnets, motors, generators, and transformers.

The primary limitation of Ampere’s law is that it is applicable in magnetostatics and is valid for steady current, i.e., the electric field does not change with time. However, Maxwell modified Ampere’s law by introducing displacement current. It is the quantity ∂D/∂t appearing in Maxwell’s equations and is defined in terms of the rate of change of D, the electric displacement field. Maxwell added this term to the electric-current term in Ampere’s law and used the amended version to derive the electromagnetic wave equation, which formed the basis for Maxwell’s equations.