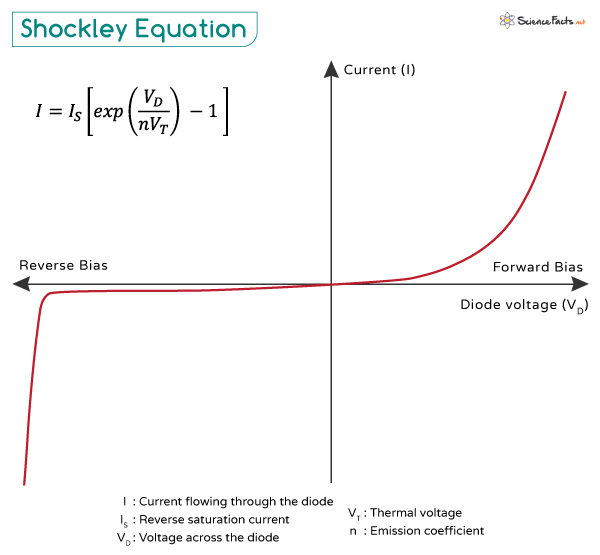
Shockley Equation

Shockley equation is a fundamental expression in semiconductor physics that describes the relationship between the current flowing through a diode and the voltage across it. The equation provides a mathematical model that predicts the behavior of p-n junction diodes under various conditions.

The equation is named after American inventor and physicist William Shockley, who was one of the inventors of the transistor in 1947.

Representation

Shockley equation considers the intrinsic material properties like the reverse saturation current and the thermal voltage. It is represented as follows:

\[ I = I_S \big[ e^{\frac{V_D}{nV_T}} – 1 \big] \]

Where:

– I is the current flowing through the diode.

– I_S is the reverse saturation current, a small constant current that flows when the diode is reverse biased.

– V_D is the voltage across the diode.

– V_T is the thermal voltage, a quantity that depends on temperature and is given by V_T = T/11,586.

– n is the emission coefficient, which is 1 for germanium and 2 for silicon.

Graph

The IV characteristic curve shows an exponential increase in current when the diode is forward-biased (positive current), allowing significant current to flow through the device. In contrast, when the diode is reverse-biased, the current remains very small and negative, corresponding to the reverse saturation current. The graph below helps visualize how the Shockley equation models the diode’s transition from a high-resistance state in reverse bias to a low-resistance state in forward bias.

Approximations

Forward Bias

The forward bias approximation is a key simplification of the Shockley equation in the forward biased region of the IV characteristic curve. Under this condition, the voltage across the diode (V_D) is positive, and the exponential term in the Shockley equation dominates the expression for current.

\[ e^{\frac{V_D}{nV_T}} >> 1 \]

It allows us to approximate the diode current as:

\[ I = I_S e^{\frac{V_D}{nV_T}} \]

This approximation is valid when the forward bias voltage is significantly larger than the thermal voltage, typically around 26 mV at room temperature.

Reverse Bias

The reverse bias approximation is another simplification of the Shockley equation that applies when a diode is reverse biased, meaning the voltage across the diode is negative. In this situation, the exponential term in the Shockley equation becomes very small since V_D is negative, making the −1 term dominate the expression.

\[ e^{\frac{V_D}{nV_T}} << 1 \]

The Shockley equation is approximated as:

I ≈ – I_S

Thus, the diode ideally allows only a very small current to flow. This current is approximately equal to the negative of the reverse saturation current, typically in the range of nanoamperes (nA) for silicon diodes.