Radioactive Decay
Radioactive decay, also known as nuclear decay, radioactivity, or radioactive disintegration, is a fundamental process in nuclear physics. It is a process in which an unstable atomic nucleus loses energy to become stable. It is a natural process and is important for medical imaging and determining the age of rocks and fossils.
What Happens During Radioactive Decay
Radioactivity occurs when an atom has an excess of energy, mass, or both, making its nucleus unstable. To reach a lower, more stable energy level, it releases energy in the form of radiation. This radiation can be emitted as particles or electromagnetic waves, depending on the nature of the decay.
The original unstable atom, known as the parent isotope, undergoes a transformation. As it loses energy, the nucleus may change in composition, such as by altering the number of protons or neutrons. This change leads to the formation of a new atom called the daughter isotope. The daughter isotope is usually more stable than the parent, but in some cases, it may still be radioactive and continue to decay until a stable form is reached.
The process of radioactive decay is random, meaning it is impossible to predict exactly when a particular atom will decay. However, for a large number of atoms, the rate of decay is consistent and can be characterized by the substance’s half-life – the time it takes for half of the atoms in a sample to decay.
Which Materials Undergoes Radioactive Decay
Radioactive decay occurs in materials that contain radioactive isotopes, which are unstable forms of elements. This instability arises because the forces holding the nucleus together are not balanced, often due to an excess of protons, neutrons, or both. To reach a more stable state, the nucleus undergoes radioactive decay.
Examples of radioactive isotopes are:
- Uranium-238 and Uranium-235
- Thorium-232
- Radium-226
- Carbon-14
- Plutonium-239
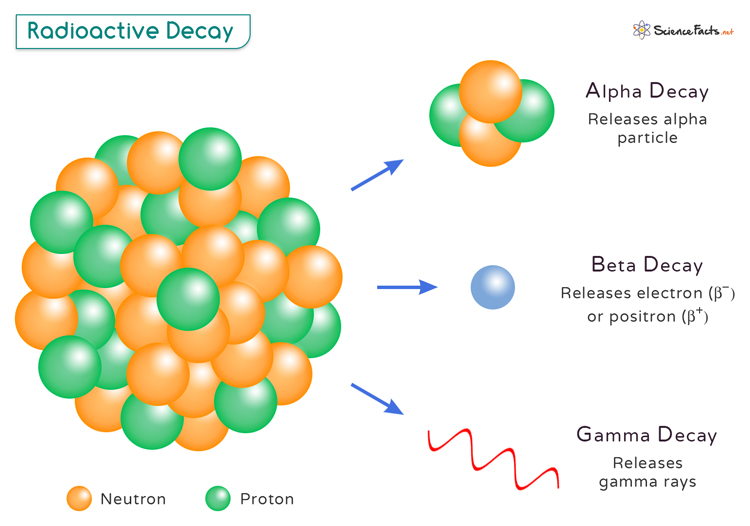
Types of Radioactive Decay
Several different types of radioactive decay can occur in nature. The three main types are:
- Alpha Decay: In alpha decay, an atomic nucleus emits an alpha particle consisting of two protons and two neutrons. This type of decay is common in heavy, unstable nuclei, as it helps to reduce the nucleus’ mass and energy.
- Beta Decay: Beta decay occurs when a neutron in the nucleus is converted into a proton, an electron, and an antineutrino. There are two main types of beta decay – beta minus and beta plus. Beta minus decay results in the emission of an electron (e–), while beta plus decay leads to the emission of a positron (β+).
- Gamma Decay: Gamma decay does not involve the emission of any particles. Instead, it occurs when an excited nucleus releases excess energy through high-energy electromagnetic radiation called gamma rays. This type of decay often follows other forms of radioactive decay.
Other types of radioactive decay are:
- Electron Capture: An inner orbital electron is captured by the nucleus, where it combines with a proton to form a neutron, releasing a neutrino in the process. As a result, the atomic number decreases by 1, but the mass number remains unchanged, leading to the formation of a new element.
- Neutron Emission: The nucleus emits one or more neutrons. It occurs if the nucleus is rich in neutrons. As a result, the mass number decreases by 1, but the atomic number remains unchanged, leading to the formation of a different isotope of the same element.
- Proton Emission: A rare type of nuclear decay in which the nucleus emits a proton. As a result, the atomic number decreases by 1, and the mass number decreases by 1, leading to the formation of a different element.
Radioactive Decay Law
The radioactive decay law is a fundamental principle that describes how the number of radioactive nuclei in a sample decreases over time. It states that the rate at which a radioactive substance decays is directly proportional to the number of undecayed nuclei present at any given time. This law is mathematically expressed through the radioactive decay differential equation:
Where
– N (t) is the number of undecayed nuclei at time t
–
– λ is the decay constant, a positive value that is specific to each radioactive isotope
The solution to the differential equation is the radioactive decay equation:
Where
– No is the initial number of nuclei
This shows that the number of undecayed nuclei decreases exponentially over time. Using the radioactive decay formula, scientists can accurately predict the amount of radioactive material remaining after a given period of time.
Half-life
As mentioned before, the half-life is the time required for half of the nuclei in a sample to decay. It is denoted by t1/2 and is related to the decay constant by the relationship:
The half-life is a statistical measure that helps predict how long it will take for a significant portion of the material to decay.
Applications of Radioactive Decay
- Radioactive Dating: Used in archaeology, geology, and paleontology to determine the age of rocks, fossils, and artifacts.
- Medical Imaging: Techniques like PET (Positron Emission Tomography) and SPECT (Single Photon Emission Computed Tomography) use radioactive tracers to visualize and diagnose diseases.
- Cancer Treatment: Radioactive isotopes are used in radiation therapy to target and destroy cancer cells.
- Sterilization: Radioactive sources like Cobalt-60 or Cesium-137 sterilize medical equipment and supplies.
- Tracer Studies in Chemistry: Radioactive isotopes serve as tracers to monitor chemical reactions, track fluid flow, and study metabolic processes.
- Smoke Detectors: Americium-241, an alpha emitter, ionizes air particles in smoke detectors, triggering an alarm when smoke is present.
- Industrial Gauges: Radioactive sources like Cobalt-60 measure the density and thickness of materials in industrial applications.
- Nuclear Power Generation: Nuclear reactors use controlled radioactive decay to generate heat, which is then converted into electricity.
- Food Preservation: Irradiation exposes food to controlled amounts of radiation to kill bacteria, insects, and parasites, extending shelf life.
- Space Exploration: Radioisotope thermoelectric generators (RTGs) use heat from radioactive decay to power spacecraft and deep-space probes.
Example Problems with Solutions
Problem 1
A piece of ancient wood is found to have a carbon-14 content that is 25% of that found in living wood. The half-life of carbon-14 is approximately 5730 years.
(a) Estimate the age of the wood.
(b) If the original carbon-14 content of the sample was 1.5 micrograms, how much carbon-14 remains in the sample?
Solution
(a) Given:
Initial fraction of carbon-14: N0 = 100%
Remaining fraction of carbon-14: N(t) = 25%
Half-life of carbon-14: t1/2 = 5730 years
Using the formula:
The decay constant is given by:
To determine the age of the wood, we use this formula.
Rearranging the terms:
The age of the wood is approximately 11,457 years.
(b) Given
Initial fraction of carbon-14: No = 1.5 microgram
Decay constant: λ = 1.29 x 10-4 years-1
Time: t = 11,457 years
Again, using the formula:
We get
The remaining amount of carbon-14 in the sample is 0.375 micrograms.
Problem 2
A sample of a radioactive isotope has an initial activity of 800 disintegrations per second. After 10 hours, the activity drops to 200 disintegrations per second.
(a) Determine the half-life of the isotope.
(b) Calculate how much time will be required for the activity to drop to 25 disintegrations per second.
Solution
(a) Given
Initial activity: N0 = 800 disintegrations per second
Activity after 10 hours: N(t) = 200 disintegrations per second
Time: t = 10 hours
The relationship between the activity and time is given by:
Rearranging the terms and replacing λ with t1/2
Putting the values
The half-life of the isotope is 5 hours.
(b) Given
Initial activity: N0 = 800 disintegrations per second
Activity after t hours: N(t) = 25 disintegrations per second
Half-life: t1/2 = 5 hours
We use the following equation
Putting the values
It will take 25 hours for the activity to drop to 25 disintegrations per second.
-
References
Article was last reviewed on Monday, August 12, 2024