Uniform Circular Motion

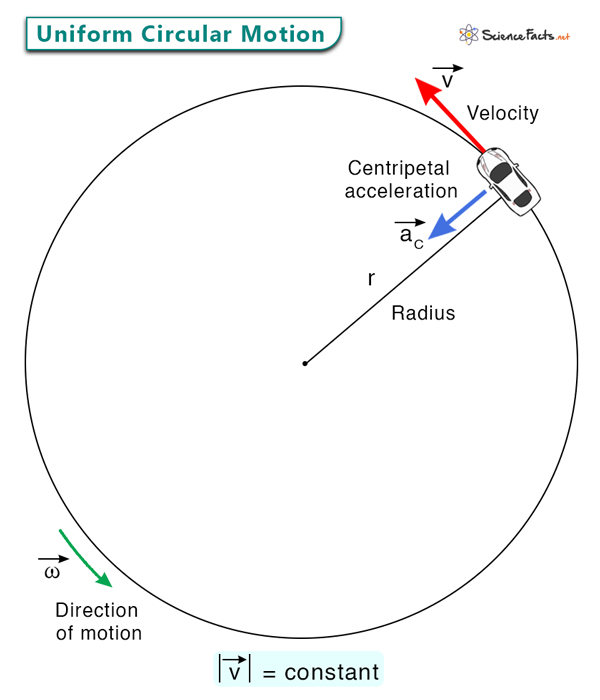
A circular motion refers to an object’s motion in a circular path. Uniform circular motion occurs when the object moves at a constant linear speed.

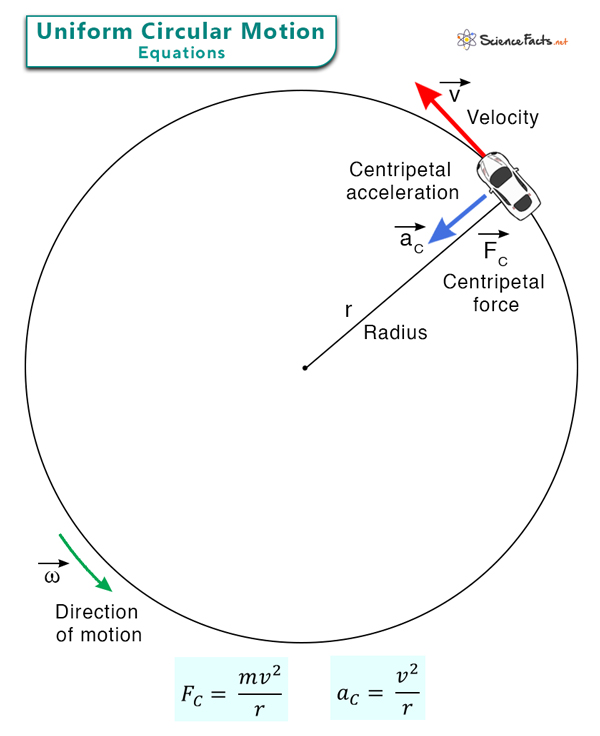
An object prescribing a circular path has a well-defined velocity with magnitude and direction. Uniform circular motion is a specific case in which the velocity remains constant in magnitude (speed) but not direction. The direction is tangential to the circle and changes as the object changes its position, resulting in acceleration. This acceleration is called centripetal acceleration. It is directed inward, radially toward the center of the circle.

An object moving in a circle is subjected to a net force. The net force is directed inward; otherwise, the object will move straight. This force is called centripetal force. It is responsible for keeping the object in its circular path. Like the centripetal acceleration, the centripetal force is directed toward the center of the circular path. This direction is always perpendicular to the velocity.

Examples

Many examples of uniform circular motion can be observed in everyday life.

The second, minute, and hour arms of a clock
Artificial satellites revolving around the Earth
Blades of a windmill

Equation

As mentioned, an object executing a uniform circular motion moves in a circle. Suppose r is the radius of the circle and T is the time period, which is the time taken to make one complete revolution. The distance covered within this time is the circumference of the circle 2πr, and the circumference divided by time gives the linear velocity v.

v = 2πr/T

A similar equation relates the magnitude of the acceleration to the linear velocity.

a_C = 2πv/T

Combining these two equations gives

a_c = v²/r

Also, the relationship between the linear and angular velocity ω is as follows.

v = ωr

The centripetal acceleration becomes

a_c = ω²r

Even if the linear velocity is constant, the object still has acceleration. It is unlikely to happen in linear kinematics, where a constantly moving object has zero acceleration.

When the centripetal acceleration is multiplied by the mass, we get the centripetal force F_C.

F_C = mv²/r = mω²r

Nonuniform Circular Motion

A circular motion is considered nonuniform if the linear velocity changes with time. As a result, the object shows acceleration in the direction of motion. This acceleration is known as linear or tangential acceleration. In the case of uniform circular motion, the tangential acceleration is zero.

Example Problems

Problem 1. A 2.5 kg mass attached to a light string rotates on a horizontal frictionless table. The radius of the circle is 1.2 m, and the string can support a mass of 25 kg before breaking. What range of speeds can the mass have before the string breaks?

Solution

Given m = 2.5 kg, r = 1.2 m, and m_Max = 25 kg

We can calculate the maximum tension F_Max of the string by assuming a mass of 25 kg attached to the string and rotating vertically. In this case, the acceleration is due to gravity.

F_Max = m_Max x g

=> F_Max = 25 kg x 9.81 m/s²= 245.25 N

We can calculate the maximum velocity v_max from the centripetal force equation.

F_Max = mv²_Max/r

=> v²_Max = F_Max x r/m

=> v_Max = √245.25 N x 1.2 m/2.5 kg = 10.85 m/s

References
- 1. Uniform Circular Motion – Openstax.org
  2. Uniform Circular Motion – Physicsclassroom.com
  3. Uniform Circular Motion and Centripetal Acceleration Review – Khanacademy.org
  4. Uniform Circular Motion – Pressbooks.online.ucf.edu
  5. More On Uniform Circular Motion – Imagine.gsfc.nasa.gov
  6. Uniform Circular Motion – Study.com