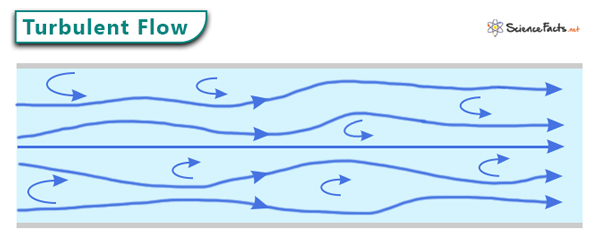
Turbulent Flow

Examples of turbulence can be observed in everyday life. These include: 

• Swirling water currents in rivers 
• Gusts of wind during storms
• Rise of cigarette smoke
• Blood flow in arteries
• Oil transport in pipelines

These natural phenomena demonstrate how turbulence affects our surroundings and influences various processes. Understanding turbulent flow is crucial in various fields, including engineering, physics, and even biology.

Turbulent flow is characterized by its chaotic and erratic nature, displaying various complex behaviors. One key feature of turbulent flow is its velocity fluctuations, with rapid flow speed and direction changes at various points in the fluid. These fluctuations give rise to vortices and eddies, which are swirling structures of different sizes. Eddies enable the mixing and diffusion of particles within the fluid, leading to enhanced transport phenomena.

Another essential characteristic is energy dissipation across various scales – from large-scale eddies to smaller dissipative structures. This energy dissipation contributes to the high levels of fluid layer mixing typically observed in a turbulent flow. Turbulent flow is known for its complex and unpredictable behavior, making it a challenging phenomenon to study and analyze accurately.

Three regimes define the fluid flow. These are laminar, transitional, and turbulent. Laminar flow is also referred to as streamline or viscous flow. It is the slow and steady movement of the fluid characterized by particles moving in straight lines within parallel layers. 

Calculating the Reynolds number is the most common method to determine the flow regime. Reynolds number is a dimensionless parameter determining the transition between laminar and turbulent flow. Reynolds number is a numerical interpretation of the correlation between inertia and viscous forces, and mathematically, represented by the ratio between the two forces. 

Where

ρ is the density of the fluid

V is the velocity of the flow

L is the characterizing length in the flow system (usually the diameter of the pipe)

μ is the viscosity of the fluid

This dimensionless number helps determine whether a fluid flow will be laminar or turbulent based on its velocity, density, viscosity, and characteristic length. Higher velocities and lower viscosities tend to promote turbulent flow. Also, larger pipe diameters can cause turbulence. The following conditions determine the flow regime in a pipe based on the Reynolds number:

• When Re < 2300, flow is laminar
• When 2300 ≤ Re ≤ 4000, flow is transitional
• When Re > 4000, flow is turbulent

In summary, when the viscous forces are pronounced, they are adequate to keep all the fluid particles in line, and the flow is laminar. When the inertial forces dominate over the viscous forces, the flow is turbulent. Laminar and turbulent flows can exist in the same conduit when operated at different flow rates. Also, suppose the flow has a different geometry, such as flow in a square duct or over a turbine blade. In that case, the transition will occur at different values of the Reynolds number.

In turbulent flows, another critical factor to consider is the friction factor. It quantifies the resistance to flow caused by the roughness of surfaces or internal obstructions within pipes or channels. 

Darcy–Weisbach equation gives a relationship between the pressure loss or head loss due to friction along the given length of pipe to the average velocity of the fluid flow for an incompressible fluid. This equation contains a dimensionless friction factor, known as the Darcy friction factor, which can be determined using empirical equations derived from extensive experimental data.

An engineering application of turbulent flow is the presence of dimples on a golf ball. In laminar flow, the boundary layer separation occurs faster. The drag to the ball is significantly higher in laminar flow, and hence the ball travels smaller distances. Researchers have found that turbulence is the solution. The separation is slowed by introducing dimples, reducing drag, and making the ball travel longer.