Kepler’s First Law

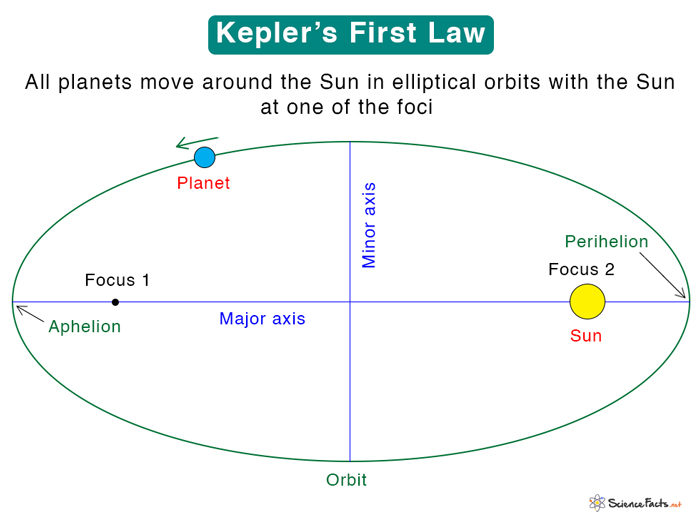
Kepler’s first law states that “All planets orbit around the Sun in a path described by an ellipse such that the Sun at one of its two foci“.

For example, the Earth moves around the Sun in an elliptical orbit. Hence, it is also known as the Law of Ellipses. The point at which a planet is closest to the Sun is called perihelion, and the point at which it is farthest is called aphelion.

Let us try to understand what an ellipse is. An ellipse is a closed curve in two dimensions that looks like a stretched-out circle. Unlike a circle that has a center, an ellipse consists of two foci and passes through a set of points such that the sum of the distance from each point to the two foci is constant.

Equation

An ellipse is represented in polar coordinates (r, θ) by the following equation:

\[ r = \frac{p}{1 + \epsilon \space \text{cos } \theta} \]

Where,

p : semi-latus rectum

ε : eccentricity

Eccentricity predicts how much the ellipse is stretched out from a circle. It takes a value between 0 (for circle) and 1 (for parabola). As the ellipse is stretched out, it gets more eccentric. The focus is further away from its center.

For a planet orbiting the Sun, r is the distance from the Sun to the planet, and θ is the angle between the planet’s current position and its closest approach, with the Sun as the vertex. Thus, r represents the orbit’s size.

At perihelion, θ = 0˚C and r is minimum.

\[ r_{min} = \frac{p}{1 + \epsilon} \]

At aphelion, θ = 180 ˚C and r is maximum.

\[ r_{max} = \frac{p}{1 – \epsilon} \]

The image below shows that the perihelion and the aphelion are at the opposite ends of the orbit. The major axis of the ellipse is the distance between them, and half of it is the semi-major axis that is represented by a.

\[ a = \frac{r_{min} + r_{max}}{2} \\ \Rightarrow a = \frac{\frac{p}{1 + \epsilon} + \frac{p}{1 – \epsilon}}{2} \\ \Rightarrow a = \frac{p}{1 – \epsilon^2} \]

Perpendicular to the major axis is the minor axis. Half the minor axis is the semi-minor axis, represented by b. It is given by the geometric mean of r_min and r_max.

\[ b = \sqrt{r_{min} \times r_{max}}\\ \Rightarrow b = \sqrt{\frac{p}{1 + \epsilon} \times \frac{p}{1 – \epsilon}}\\ \Rightarrow b = \frac{p}{\sqrt{1 – \epsilon^2}} \]

From the expressions for a and b, we find that

\[ pa = b^2 \]

The shape of the orbit is of less significance than the position of the Sun within an orbit. The eccentricity is essential, as it defines how much closer or further the planet can be at perihelion or aphelion than on the average. It is given by the coefficient of variation between r_min and r_max.

\[ \epsilon = \frac{r_{max} – r_{min}}{r_{max} + r_{min}} \]

The eccentricity can also be written in terms of the semi-major and the semi-minor axes.

\[ \epsilon = \sqrt{1-\Big ( \frac{b}{a} \Big )^2} \]