Kepler’s Laws
Kepler’s laws of planetary motion are a set of three laws describing the motion of planets around the Sun. German mathematician and astronomer Johannes Kepler published these laws between 1609 and 1619 based on observations made by his mentor, Danish astronomer Tycho Brahe. Although Kepler applied the three laws to planets in the solar system, they can be extended to planets outside the solar system, asteroids, and artificial satellites. These laws are collectively known as First Law, Second Law, and Third Law.
Explanation of the Three Laws
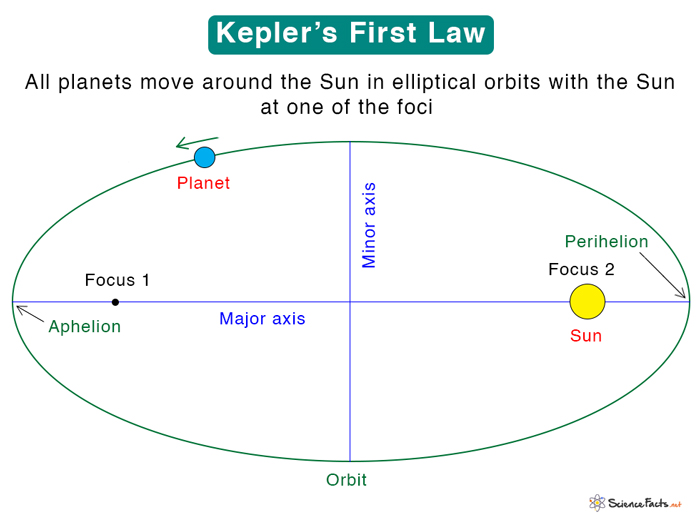
1. First Law
Statement: “All planets orbit around the Sun in a path described by an ellipse with the Sun at one of its two foci“.
Also known as the Law of Ellipses, Kepler concluded that all solar system planets have elliptical orbits. The Sun’s center is at one of the foci. When a planet revolves around the Sun, its distance from the Sun constantly changes. The point of the closest approach to the Sun is the perihelion, and the furthest point is the aphelion. Kepler’s first law is used to study the trajectories of planets, asteroids, and comets by applying the ellipse equations.
Equation
The equation of an ellipse in a polar coordinate (r, θ) system is
Where,
p : semi-latus rectum
ε : eccentricity
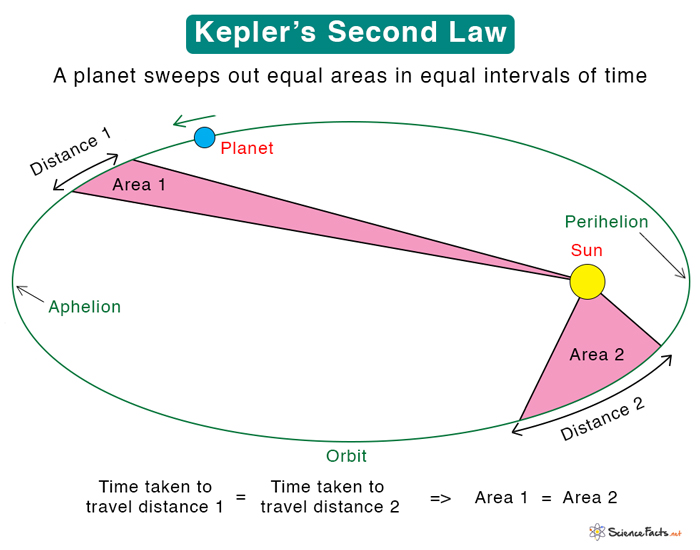
2. Second Law
Statement: “An imaginary line joining a planet and the Sun sweeps out equal areas in equal time intervals“.
Also known as the Law of Equal Areas, this law implies that the areal velocity of the revolving planet remains constant. In other words, planets do not move at a constant speed in their orbits. A line segment joining the planet and Sun sweeps out equal parts in equal time intervals. Hence, the speed of the planet at perihelion is higher than at aphelion. Kepler’s second law is applied to study the angular speeds at different points on the trajectory and the magnitude of acceleration.
Equation
The areal velocity is the area swept by the planet’s orbit divided by the time taken to sweep it. The following expression gives its value.
Where
dA/dt : Areal velocity
L : Angular momentum of the planet
m : Mass of the planet
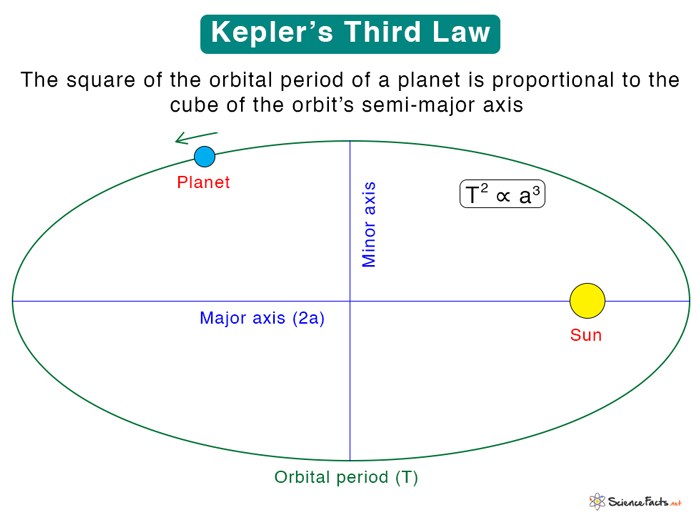
3. Third Law
Statement: “The square of a planet’s orbital period is directly proportional to the cube of the orbit’s semi-major axis“.
Also known as the Law of Harmonies, this law implies that the orbital period increases rapidly with the orbit’s semi-major axis. The ratio of the squares of the periods to the cubes of the semi-major axes is the same for each planet. Kepler’s third law is used to study the orbital periods and planet’s mass.
Equation
Suppose T is the orbital period and a is the semi-major axis of the elliptical orbit. Then,
If T is expressed in Earth years and a in astronomical unit (A.U.), then k = 1.
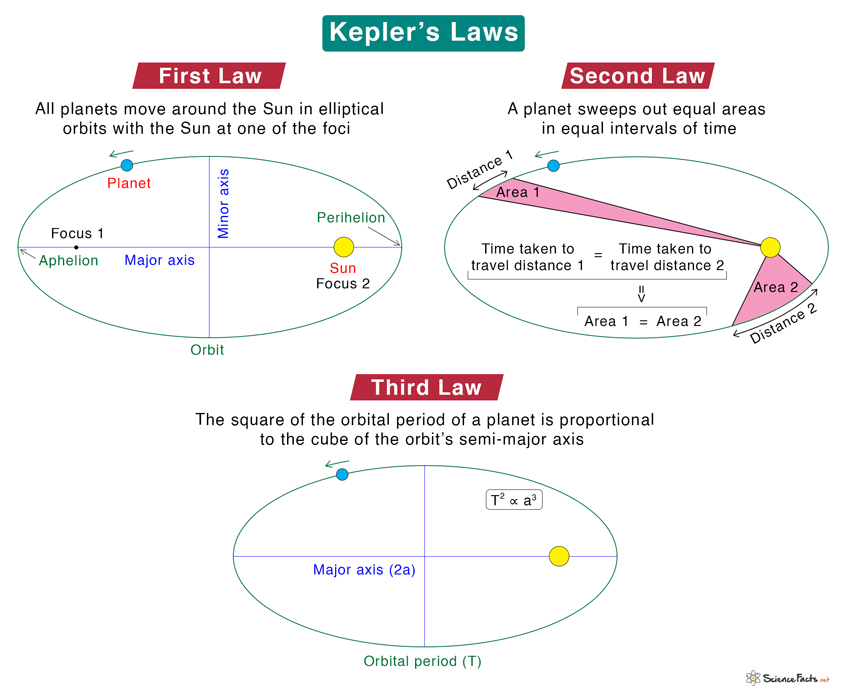
The following image summarizes all three laws.
-
References
Article was last reviewed on Thursday, February 2, 2023