Fundamental Frequency
Definition: What is Fundamental Frequency?
The lowest or base frequency produced by any instrument producing sound is known as the fundamental frequency. Typically, it is the lowest resonant frequency of any vibrating object that displays a periodic waveform.
A sine wave is the simplest of all waveforms and contains only a single fundamental frequency. Almost all musical sounds have waves that are noticeably more complex than a sine wave. It is the addition of harmonics and overtones to a wave that makes it possible to distinguish between different sounds and instruments.
What are Harmonics?
Most vibrating objects have more than one resonant frequency, and those used in musical instruments typically vibrate at higher frequencies called harmonics. Harmonics are defined as unwanted higher frequency components that are integral multiples of the fundamental frequency and have lower amplitudes (volume) than the fundamental frequency. Harmonics distort the fundamental waveform of the instrument.
Vibrating strings, open cylindrical air columns, and conical air columns will vibrate at all harmonics of the fundamental. Cylinders with one end closed will vibrate with only odd harmonics of the fundamental (discussed later). Vibrating membranes typically produce vibrations at harmonics, but also have some resonant frequencies which are not harmonics.
The fundamental frequency is also called the first harmonic of the instrument. Overtones are frequencies of a waveform that are higher than, but not directly related to, the fundamental frequency.
Key Terms | |
| Fundamental Frequency | The lowest frequency produced by any particular instrument is known as the fundamental frequency |
| Harmonic | A harmonic is a waveform whose frequency is an integral multiple of the fundamental frequency |
| Node | A point along a standing wave where the wave has a minimum amplitude |
| Antinode | A point along a standing wave where the wave has a maximum amplitude |
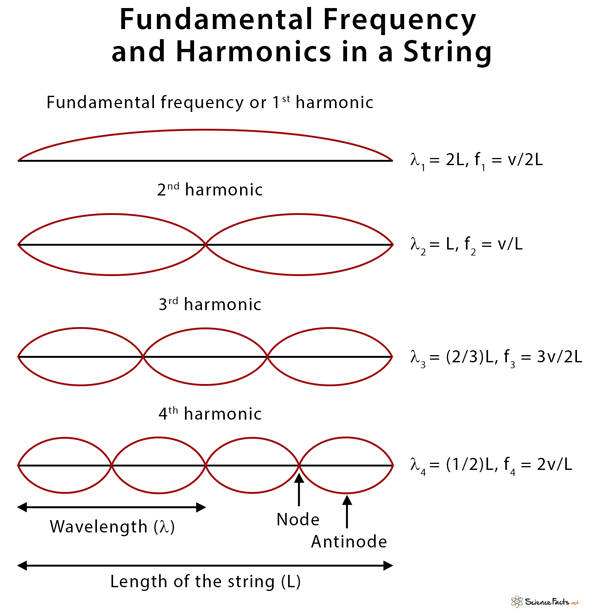
Fundamental Frequency and Harmonics in a String
In the case of a string, since its ends are fixed, it has zero displacements at the ends. These are known as nodes. The relationship between the wavelength (λ) and the length (L) of the string is as follows: λ = (2/n) L, where n is a whole number. In other words, there can be half a wave on the string (n = 1), one wave (n = 2), and one and a half waves (n = 3). However, there can never be any other fraction of a wave because that would require not having a node at both ends.
Higher harmonics have nodes in other locations besides just at the ends. In between two nodes, there is a region where the vibrations are a maximum, and it is called antinode. The fundamental frequency has one antinode, and the 2nd harmonic has two antinodes.
A string has several frequencies at which it will naturally vibrate. The natural frequency at which the string vibrates depends upon its tension, linear density, and length of the string. Once the string density and tension are chosen, the speed is fixed, and the frequencies will depend on the wavelength, as shown in the following table. The harmonics are all multiples of the fundamental frequency.
Fundamental Frequency and Harmonics in a String | ||
| Harmonic number | Wavelength | Frequency |
|---|---|---|
| 1 (fundamental) | λ1 = 2L | f1 = v/2L |
| 2 | λ2 = L | f2 = v/L = 2f1 |
| 3 | λ3 = (2/3)L | f3 = 3v/2L = 3f1 |
| 4 | λ4 = (1/2)L | f4 = 2v/L = 4f1 |
| n | λn = (2/n)L | fn = nv/2L = nf1 |
Fundamental Frequency and Harmonics in a Tube
Sound waves are a common phenomenon in air columns, tubes, and pipes. In a tube or pipe, if an end is open, the air can move freely, and so there is a displacement antinode at that end.
Open Tube
When the two ends of a tube are open, it is called an open tube. The fundamental frequency of such a tube has a maximum displacement (antinode) at each end and a zero displacement (node) in the middle. For a tube of length L that has an antinode on each end, the relationship between wavelength (λ) and length (L) of the tube is λ = (2/n) L, where n is a whole number. The pressure profile in an open tube gives harmonics precisely the same as a string.
Fundamental Frequency and Harmonics in an Open Tube | ||
| Harmonic number | Wavelength | Frequency |
|---|---|---|
| 1 (fundamental) | λ1 = 2L | f1 = v/2L |
| 2 | λ2 = L | f2 = v/L = 2f1 |
| 3 | λ3 = (2/3)L | f3 = 3v/2L = 3f1 |
| 4 | λ4 = (1/2)L | f4 = 2v/L = 4f1 |
| n | λn = (2/n)L | fn = nv/2L = nf1 |
Closed Tube
Musical instruments are made of a tube that is closed at one end but opened at the other. Such a tube is known as a closed tube. At the closed end, the air cannot move, so there is a displacement node. For a tube of length L that has a displacement node at the closed end, the wavelength is given by λ = (4/n) L, where n is a whole number. This value is twice the lowest wavelength occurring in a tube with two open ends. The requirement of having a node at the closed end means that the even-numbered frequencies will be missing from a closed tube. Only odd harmonics are present.
Fundamental Frequency and Harmonics in a Closed Tube | ||
| Harmonic number | Wavelength | Frequency |
|---|---|---|
| 1 (frequency) | λ1 = 4L | f1 = v/4L |
| 2 | Missing | Missing |
| 3 | λ3 = (4/3)L | f3 = 3v/4L = 3f1 |
| 4 | Missing | Missing |
| n = odd | λn = (4/n)L | fn = nv/4L = nf1 |
So, for a tube open on both ends, the available frequencies are an integral multiple of the fundamental frequency such as f1, 2 x f1, and 3 x f1. However, for a tube that is closed on one end, only odd multiples of the fundamental frequency are observed, such as f1, 3 x f1, and 5 x f1.
One can compare the tables for the open and closed tubes. For a given length L, the closed tube has a lower fundamental frequency or longer wavelength and has only odd frequencies. This condition affects the available frequencies of the instrument, and so affects the tone. Most tube instruments, like an organ pipe, are closed on one end because the musician playing the instrument has their mouth over one end.
-
References
Article was last reviewed on Friday, February 17, 2023